# load packages and data
library (bmmb)
library (brms)
data (exp_data)
# exclude actual men and apparent men
notmen = exp_data[exp_data$C_v!='m' & exp_data$C!='m',]6 Variation in parameters (‘random effects’) and model comparison
In Chapter 4, we introduced ‘random effects’. These were intercept terms that were specific to ‘sources’ of data (e.g. listener, speaker), and fit using adaptive partial pooling. We used speaker and listener-dependent intercepts because we know that each listener, and each speaker, in our data can be associated with unpredictably different average apparent heights. In Chapter 5 we built models that compared two groups of measurements by including a single predictor that-distinguished the groups. However, our models assumed that the difference between the groups, the effect of the single predictor, was fixed across all listeners. In this chapter, we will build models that allow for listener-specific variation in fixed-effects predictors in addition to the intercept. Then, we will discuss how to evaluate whether the increasing complexity of our model is making our model ‘better’ and whether it’s justified by our data.
6.1 Chapter pre-cap
In this chapter, we introduce interactions as conditional effects, and marginal (average) effects are introduced as ‘main’ effects. The concepts of crossing and nesting are presented and the importance of crossing for the estimation of interactions is discussed. We then outline models with multiple group-dependent parameters (‘random effects’) and the interpretation of these as interactions. We introduce the multivariate normal distribution, in addition to the concepts of multidimensionality and correlation. The fact that random effects are drawn from multivariate normal distributions is discussed, as are related topics for multilevel models (e.g. the specification of priors for correlation matrices). After that, this chapter focuses on model comparison. We contrast in-sample and out-of-sample prediction and discuss the bias-variance trade-off. Finally, we present the widely applicable information criterion (WAIC) and leave-one-out cross-validation, and discuss model selection.
6.2 Data and research questions
We’re going to use the same data from the Chapter 5, again excluding adult males and focusing only on the apparent height of adult females, girls and boys. We’re going to build models that expand on those of Chapter 5 to ask the same questions:
(Q1) How tall do speakers perceived as adult females sound?
(Q2) How tall do speakers perceived as children sound?
(Q3) What is the difference in apparent height associated with the perception of adultness?
Below we load the data and exclude all apparent and veridical adult males.
The relevant variables in our data frame are:
L: An integer from 1 to 15 indicating which listener responded to the trial.height: A floating-point number representing the height (in centimeters) reported for the speaker on each trial.S: An integer from 1 to 139 indicating which speaker produced the trial stimulus.A: The apparent age of the speaker indicated by the listener,a(adult) orc(child).
We recreate Figure 5.9 as Figure 6.1 below to show the distribution of apparent height by listener and across apparent ages. In Chapter 5, we focused on ‘the difference’ between height judgments for apparent adults and apparent children as a singular thing. This is a bit like focusing only on the difference between the boxes in the left plot of Figure 6.1. However, if we instead focus on the right plot in Figure 6.1 we see that there is not a single difference in apparent heights between apparent children and adults, but rather a set of listener-specific differences. The model we will introduce in this chapter will be able to represent this information.
show plot code
par (mfrow = c(1,2), mar = c(4.1,.1,.5,.1),oma = c(0,4,0,.50)); layout (mat = t(c(1,2)), widths = c(.2,.8))
boxplot (height ~ A, data=notmen, col = c(beige,lightpink),ylim = c(103,185), xlab="")
mtext (side=1, "Apparent Age Group", line=3)
abline (h = c(155.3,155.3+8.8,155.3-8.8), lwd = c(3,2,2), col = c(1,4,3))
boxplot (height ~ A, data=notmen, col = c(beige,lightpink),ylim = c(103,185), xlab="",add=TRUE)
mtext (side = 2, outer = FALSE, "Apparent height (cm)", line = 2.75)
boxplot (height ~ A+L, data=notmen, col = rep(bmmb::cols,each=2),ylim = c(103,185),
ylab="",yaxt="n", xaxt="n",xlab="Listener")
axis (side=1, at = seq(1.5,30.5,2), 1:15)
abline (h = c(155.3,155.3+8.8,155.3-8.8), lwd = c(3,2,2), col = c(1,4,3))
boxplot (height ~ A+L, data=notmen, col = rep(bmmb::cols,each=2),ylim = c(103,185),
ylab="",yaxt="n", xaxt="n",xlab="Listener", add = TRUE)
6.3 Variation in parameters across sources of data
The models we fit in Chapter 5 included a predictor representing the apparent age of the speaker. However, this was only a population-level parameter (i.e. a ‘fixed’ effect) meaning that it had the same value for all listeners. Another way to think about this is that our model included only the marginal effect for apparent age. This is the effect of apparent age on average across all listeners, independent of listener. This sort of effect is often referred to as a main effect. Someone might ask “what is the average apparent height difference between apparent children and adult females?” and you might say “about 20 cm”. Which listener exactly does this statement apply to? To all of them, this is the average overall effect.
In contrast, we may want to think about the effect of apparent age conditional on the listener. For example, imagine that this effect varies conditionally based on the listener such that it is large for some listeners and small for others. In this case, if someone asks “what is the apparent height difference between apparent children and adult females?” you may have to answer “well it depends on the listener”. When the effect of one predictor varies based on the value of another predictor, these predictors are said to interact or to have an interaction. The parameters in your model that help you capture these conditional effects are referred to as interactions or interaction effects. The ‘fixed’ effect for A1 we included in our models in Chapter 5 really represents the marginal (overall) effect for the predictor. To investigate the values of this predictor conditional on the listener, we need to include the listener by A1 interaction in our model. We denote interaction terms in our models using a colon (:) where A:B can be read ‘A given B’ or ‘A conditional on B’.
We can find the average apparent height reported by each listener for each apparent age (a adult, or c child) using the code below:
round ( tapply (notmen$height, notmen[,c("A","L")], mean) )
## L
## A 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
## a 167 167 164 161 162 166 163 165 166 165 165 168 168 168 165
## c 162 142 132 154 141 148 149 140 140 138 155 148 134 146 148The average of each column is the average apparent height reported by each listener across both apparent ages. The average across each row is the average apparent height reported for each apparent age, across all listeners. Each individual cell represents the average apparent height reported by each listener for each apparent age, and the mean of all cells represents the overall grand mean.
In the left plot of Figure 6.2 we present the average height reported by each listener. The variation seen along the line is a result of non-zero listener effects: In the absence of listener effects, the line would be flat and horizontal at the grand mean. So, it is the listener effect (L) that gives the line its specific shape. In the middle plot, we see the average apparent height reported by each listener for each apparent age. Each line has an unpredictably different shape, and since the shape reflects the listener effect, this means that listener (L) has an unpredictable effect across the levels of apparent age (A). This suggests that our data has a meaningful interaction between listener and apparent age, L:A, which can be read as ‘the effect of listener given the level of apparent age’.
show plot code
listener_age_differences = tapply (notmen$height, notmen[,c("A","L")], mean)
par (mfrow = c(1,3), mar = c(4,4,1,1))
plot(colMeans(listener_age_differences), cex=2,
type = 'b', col = bmmb::cols[7], pch=16, ylim = c(132,177),ylab = "Apparent height (cm)",
lwd=2, xlab = "Listener",cex.axis=1.2,cex.lab=1.2)
abline (h = c(155), lty = c(1,3,3),col=bmmb::cols[7], lwd=2)
plot(listener_age_differences[1,], cex=2,
type = 'b', col = lavender, pch=16, ylim = c(127,172),ylab = "Apparent height (cm)",
lwd=2, xlab = "Listener",cex.axis=1.2,cex.lab=1.2)
lines(listener_age_differences[2,],cex=2,
type = 'b', col = deepgreen, pch=16,lwd=2)
abline (h = c(155, 165, 145), lty = c(1,2,2), col=bmmb::cols[c(7,14,4)], lwd=2)
listener_age_effects = (listener_age_differences[1,]-listener_age_differences[2,])/2
plot(listener_age_effects, lwd=2,lty=1,cex=2,cex.axis=1.2,cex.lab=1.2,
type = 'b', col = darkorange, pch=16, ylim = c(-7,28),
ylab = "Apparent height difference (cm)", xlab = "Listener")
abline (h = mean (listener_age_effects), col = darkorange, lwd=2)
# plot(listener_age_effects, lwd=1,lty=3,
# type = 'n', col = darkorange, pch=16, ylim = c(0,18),
# ylab = "Height difference (cm)", xlab = "Listener")
# arrows (1:15, rep(mean(listener_age_effects),15), 1:15, listener_age_effects,
# length=.1, lwd=2, col=skyblue)
# abline (h = mean(listener_age_effects))
In the middle plot of Figure 6.2, the broken lines represent the mean apparent heights for apparent adults and apparent children. The average (main) effect for apparent age is equal to the difference between these broken lines and the solid line representing the grand mean (or half the distance between the broken lines). This effect has an average magnitude of 10.1 cm, which we can see in the right plot of the figure. However, each listener has an unpredictable difference between their points on each line and a correspondingly unpredictable effect for apparent age in the right plot in Figure 6.2. Since the distance between the lines determines the effect for apparent age, this represents listener-dependent variation in A and a meaningful interaction between apparent age and listener (A:L) in our data.
Actually, the L:A interaction entails an A:L interaction (and vice versa): In the process of adding an A:L interaction in your data you also necessarily add an L:A interaction to your data. Imagine the middle plot in Figure 6.2 contained two flat parallel lines, separated by some amount (the effect for A). In order to add a listener-dependent age effect (A:L) to these lines, we would need to make the separation between the lines unpredictably different for each listener. However, in doing so we necessarily also make the shapes of the two lines unpredictably different. This is the only way to make the separation between the lines different for each listener. Since the shape of the line is the listener effect, by giving each line a different shape we also necessarily add an age-dependent effect for listener to our data. As a result of this, the A:L interaction is the same thing as the L:A interaction, and the notational difference between them is only superficial.
Although we can think of interactions either way, conceptually it may be useful to think of them primarily from one perspective or another. In our case, we will focus on the listener-dependent effect for apparent age, presented in the right plot of Figure 6.2. The value of each point along the line in the right plot reflects the spacing of the two lines in the middle plot of the same figure. In the complete and total absence of an interaction between listener and age, the orange line in the figure would be horizontal at 10.1 (the marginal difference). In the presence of an interaction, our marginal and listener-dependent effects may diverge in a seemingly random manner, as seen in the figure.
Before moving on, we need to discuss the concepts of crossing and nesting, and how these relate to interactions. When two factors are crossed, this means that all levels of one factor appear at all levels of the other factor. When levels of one factor appear exclusively at specific levels of the other factor they are said to be nested. To estimate the interaction between two factors, the factors should be crossed. Since our ‘random effects’ are just interactions, this means that to include a random effect for a predictor given some grouping factor (like listener), it needs to be crossed with that factor.
For example, consider a situation where (monolingual) listeners are divided into groups according to their native languages. We might imagine a model like this that tries to estimate height based on the native language (NatLang) of the listeners to see if there are reliable cross-language differences in listener’s opinions:
height ~ NatLang + (1|L)
In such an experiment, the listener factor will be nested within first language because each listener only speaks one language. As a result, in such a situation a model can estimate the ‘fixed’, marginal effect of native language on apparent height. However, this model can not estimate the listener-dependent effect of first language, i.e. the first language ‘random effect’ for listeners or the listener by native language interaction. This means that neither of the following models is possible:
height ~ NatLang + (NatLang|L)
height ~ NatLang + L + NatLang:L
The reason for this is very straightforward. If we do not observe the effect of first language for each level of listener, we are not in a position to say anything about the listener-dependent effect of first language (i.e. the conditional effect of native language for every individual listener). For example, if the first listener is an English speaker, how can you possibly estimate the conditional effect for when that listener is a Mandarin speaker? What would that even mean?
In terms of our data, this means that to estimate listener-dependent effects for apparent age we need to make sure listener is crossed with apparent age. We can do this by, for example, cross tabulating our observations of apparent age with listener (table(notmen$A, notmen$L)) and making sure that we have more than zero observations for every combination of listener and apparent age (which we do). As a result, it’s possible to estimate the interaction between these in our model. In contrast, speakers are not crossed with apparent age. If we tabulate apparent age by speakers (table(notmen$A, notmen$S)), we see a lot of cells with zero observations. This is because some speakers were just not very confusable: Some children were never identified as adults and some adults were never identified as children. As a result, our model may run into problems if it tries to estimate the interaction between speaker and apparent age, or the random effect of apparent age for each speaker.
6.3.1 Description of our model
Before including interactions in our model, let’s take a step back and consider the model formula we used in Chapter 5. Below, we explicitly include the leading one (indicating the intercept) to make the following discussion simpler.
height ~ 1 + A + (1|L) + (1|S)
This formula told our model to draw the parameter related to A from a fixed prior distribution and to draw the L and S terms from distributions whose standard deviations were estimated from the data (i.e. using adaptive partial pooling). We did this by adding L and S to the right of a pipe inside parentheses (like this (1|L)) and putting a 1 to the left of the pipe. Recall that the | symbol means ‘given’ so that the notation (1|L) says “estimate an intercept given listener”, or “estimate a different intercept effect for each level of the factor listener”. We can imagine an analogous model formula that uses only ‘fixed effects’, meaning it uses no pooling to estimate all of the listener and speaker effects. The formula for such a model would look like this:
height ~ 1 + A + L + S
As discussed above, we seem to have listener-dependent age effects in our model, suggesting that we want to include the interaction of apparent age and listener in our model. Interactions between combinations of fixed effects can be denoted using :. For example, the formula below says “include the main effect for A and L, and the interaction between A and L”. The : symbol can also be read as “given”, which helps to highlight that these represent conditional effects. So A:L can be read out loud as “A given L” or “the effect of A given the value of L”.
height ~ 1 + A + L + A:L + S
As a shortcut, we can use the symbol * which means “include the main effects for these predictors and all interactions between them.”
height ~ 1 + A * L + S
The previous two formulas include the marginal effects of age and listener and the interaction between them. However, they estimate all these without adaptive pooling. We know that it is advisable to estimate factors with large numbers of levels using adaptive pooling, regardless of how ‘random’ the effect may be (see Section 4.4). This applies not only to the marginal effects of predictors such as listener, but also to the interactions between these ‘random’ effects and our ‘fixed’ effects. In order to estimate listener-dependent age effects in our model using adaptive pooling, we include these inside the parentheses belonging to the listener predictor, like so:
height ~ 1 + A + (1 + A|L) + (1|S)
The formula above tells brms: “Height varies as a function of an intercept and an age effect, a listener-specific intercept and age effect, and a speaker specific intercept”. It also tells brms to estimate the listener intercepts, the listener age effects, and the speaker intercepts as random effects, i.e. using adaptive pooling. Notice the parallel structure between our models with and without random effects:
height ~ 1 + A + L + A:L + S
height ~ 1 + A + (1 + A |L) + (1 |S)
These models have equivalent parameters, which have been horizontally aligned in the two formulas above. The L term in the top model is represented by the 1 in (1 + A|L) in the bottom model (the listener-dependent intercept effect), and the A:L term in the top model is represented by the A in (1 + A|L) in the bottom model (the listener dependent age effect). The main difference between L and A:L on one hand and (1 + A|L) on the other, is that the latter notation tells your model to estimate these listener-dependent predictors using adaptive pooling. When our formula has non-intercept predictors, we can omit the 1 and write it as seen below:
height ~ A + (A|L) + (1|S)
Our model formula might specify a model as in Equation 6.1. Compared to the t-distributed model we fit at the end of Chapter 5, the only changes have been the addition of a new term, \(A \colon L_{[\mathsf{L}_{[i]}]}\), and its associated priors \(A \colon L_{[\bullet]} \sim \mathrm{t}(3, 0,\sigma_{A \colon L})\), and \(\sigma_{A \colon L} \sim \mathrm{t}(3,0,12)\). Note that although the \(A\) predictor does not need a subscript, the \(A \colon L_{[\mathsf{L}_{[i]}]}\) term (the by-listener random effect for age) does. This is because although we only have a single age predictor, the interaction term estimates a different one of these for each listener, which requires the estimation of 15 such parameters in our model.
\[ \begin{equation} \begin{split} height_{[i]} \sim \mathrm{t}(\nu, \mu_{[i]},\sigma) \\ \mu_{[i]} = \mathrm{Intercept} + A + L_{[\mathsf{L}_{[i]}]} + A \colon L_{[\mathsf{L}_{[i]}]} + S_{[\mathsf{S}_{[i]}]} \\ \\ \mathrm{Priors:} \\ L_{[\bullet]} \sim \mathrm{N}(0,\sigma_L) \\ A \colon L_{[\bullet]} \sim \mathrm{N}(0,\sigma_{A \colon L}) \\ S_{[\bullet]} \sim \mathrm{N}(0,\sigma_S) \\ \\ \mathrm{Intercept} \sim \mathrm{t}(3, 156,12) \\ A \sim \mathrm{t}(3, 0,12) \\ \sigma_L, \sigma_S, \sigma_{A \colon L} \sim \mathrm{t}(3, 0,12) \\ \nu \sim \mathrm{gamma}(2, 0.1) \\ \sigma \sim \mathrm{t}(3, 0,12) \\ \end{split} \end{equation} \tag{6.1}\]
For the sake of comparison, Equation 6.2 presents the model structure associated with the following formula:
height ~ 1 + A + L + A:L + S
We can see that Equation 6.1 and Equation 6.2 are nearly identical. The only difference between the two models is whether the standard deviations of the prior distributions of the listener and speaker related parameters (e.g. \(L_{[\bullet]}\)) are estimated from the data (as in Equation 6.1), or specified a priori (as in Equation 6.2).
\[ \begin{equation} \begin{split} height_{[i]} \sim \mathrm{t}(\nu, \mu_{[i]},\sigma) \\ \mu_{[i]} = \mathrm{Intercept} + A + L_{[\mathsf{L}_{[i]}]} + A \colon L_{[\mathsf{L}_{[i]}]} + S_{[\mathsf{S}_{[i]}]} \\ \\ \mathrm{Priors:} \\ L_{[\bullet]} \sim \mathrm{N}(0,12) \\ A \colon L_{[\bullet]} \sim \mathrm{N}(0,12) \\ S_{[\bullet]} \sim \mathrm{N}(0,12) \\ \\ \mathrm{Intercept} \sim \mathrm{t}(3, 156,12) \\ A \sim \mathrm{t}(3, 0,12) \\ \nu \sim \mathrm{gamma}(2, 0.1) \\ \sigma \sim \mathrm{t}(3, 0,12) \\ \end{split} \end{equation} \tag{6.2}\]
The model in Equation 6.1 is preferable over the one in Equation 6.2 because it will use information about the distribution of \(L\), \(A \colon L\), and \(S\) to estimate the associated effects. However, one potential problem is that the model in Equation 6.1 draws each of the listener-dependent effects (\(L\), \(A \colon L\)) from independent-distributions as if these were totally unrelated, and they may not be.
6.3.2 Correlations between random parameters
In Figure 6.3, we plot the listener effects, and the listener-dependent age effects originally presented in Figure 6.2. However, this time they have both been sorted based on the value of the listener effects. We can see clearly that as the listener effects increase, the age effects decrease. In the rightmost plot, we present a scatter plot of these two variables, which reinforces the fact that these variables have a negative relationship: Smaller values of apparent height tend to be associated with larger apparent age effects. This is important because, if this is true, it suggests that we are unlikely to observe listeners who reported tall speakers on average and had large age effects on height (or vice versa). This is because as seen in Figure 6.3, listeners who reported tall speakers on average tended to exhibit small age effects.
show plot code
par (mfrow = c(1,3), mar = c(4,4,1,1))
listener_age_differences = tapply (notmen$height, notmen[,c("A","L")], mean)
ord = order (colMeans(listener_age_differences))
listener_means = colMeans(listener_age_differences)
listener_age_effects = (listener_age_differences[1,]-listener_age_differences[2,])/2
par (mfrow = c(1,3), mar = c(4,4,1,1))
plot(colMeans(listener_age_differences)[ord], cex=2,
type = 'b', col = bmmb::cols[7], pch=16, ylim = c(145,167),ylab = "Apparent height (cm)",
lwd=2, xlab = "",cex.lab=1.2,cex.axis=1.2, xaxt='n')
abline (h = c(155), lty = c(1,3,3),col=bmmb::cols[7])
plot(listener_age_effects[ord], lwd=2,lty=1,cex=2,cex.lab=1.2,cex.axis=1.2,
type = 'b', col = darkorange, pch=16, ylim = c(0,22),xaxt='n',
ylab = "Apparent height difference (cm)", xlab = "")
abline (h = mean (listener_age_effects), col = darkorange)
# plot(listener_age_effects, lwd=1,lty=3,
# type = 'n', col = darkorange, pch=16, ylim = c(0,18),
# ylab = "Height difference (cm)", xlab = "Listener")
# arrows (1:15, rep(mean(listener_age_effects),15), 1:15, listener_age_effects,
# length=.1, lwd=2, col=skyblue)
# abline (h = mean(listener_age_effects))
plot(listener_means,listener_age_effects, lwd=1,lty=3,xlim=c(145,167),ylim=c(0,22),
type = 'p', col = cols[4], pch=16, ylab = "Age Effect (cm)",cex=2,
xlab = "Height Intercept (cm)",cex.lab=1.2,cex.axis=1.2)
abline (v = mean(listener_means), h = mean(listener_age_effects), lty=3)
The linear correlation between two variables (often referred to simply as the correlation) is a measure of the linear relationship between the variables. An informal (but accurate) way to think of a linear relationship is that when you make a scatter plot using two variables (as in the right plot of Figure 6.3), the organization of the points should resemble a line if there is a strong linear relationship between them. The more the dots form a single perfect line, the closer the magnitude of the correlation gets to 1. Whether the value of a perfect correlation is 1 or −1 depends on if the line is sloped up (1) or down (−1) from left to right. A correlation of 0 means there is no linear relationship between the variables. So, if two variables have a correlation of 0 you would be hard-pressed to draw any kind of line that captured the relationship between the variables (though some other curve might work). Figure 6.3 suggests that listener means and age effects are negatively correlated.
There are many ways to measure correlation, but the most common way is by using Pearson’s correlation coefficient, defined in Equation 6.3 for variables \(x\) and \(y\). We use the little hat, like this \(\hat{r}\), because this is an estimate of the correlation between our variables. Equation 6.3 introduces a term we have not seen yet, \(\sigma_{xy}\), corresponding to the covariance between \(x\) and \(y\) (often denoted by \(\mathrm{cov}(x,y)\)). We can see below that the correlation between two variables is the covariance divided by the product of their individual standard deviations (\(\hat{\sigma}_x\) and \(\hat{\sigma}_y\)).
\[ \begin{equation} \hat{r} = \frac {\hat{\sigma}_{x,y}} {\hat{\sigma}_x \hat{\sigma}_y} \end{equation} \tag{6.3}\]
The variance of a variable is the expected value of squared deviations from the mean. The covariance of two variables is the expected value of the product of their deviations of each from their respective means. The covariance of two variables of length \(n\) can be estimated by calculating the sum of the product of deviations from the mean and dividing by the number of observations minus one, as seen in Equation 6.4.
\[ \begin{equation} \hat{\sigma}_{x,y} = \frac {\Sigma(x_{[i]}-\bar{x})(y_{[i]}-\bar{y})} {(n-1)} \end{equation} \tag{6.4}\]
Replacing \(\hat{\sigma}_{xy}\) in Equation 6.3 with Equation 6.4 yields Equation 6.5, an estimate of the correlation (\(r\)) between \(x\) and \(y\).
\[ \begin{equation} \hat{r} = \frac {\Sigma(x_{[i]}-\bar{x})(y_{[i]}-\bar{y})} {(n-1) \cdot \hat{\sigma}_x \hat{\sigma}_y} \end{equation} \tag{6.5}\]
Using Equation 6.5, we can calculate Pearson’s correlation coefficient for two variables. We can do this for any two vectors in R using the cor function. Below we find the average apparent height reported by each listener, and then half the difference in apparent height reported by each listener for each apparent age (i.e. the effect for apparent age). As seen below, this tells us that the correlation between the listener means and apparent age effects is −0.85, representing a strong negative correlation between these two variables.
# find means for each listener for each apparent age
listener_age_means = tapply (notmen$height, notmen[,c("A","L")], mean)
# average of each column = listener means
listener_effects = colMeans (listener_age_means)
# half the difference across rows = listener age effects
listener_age_effects = (listener_age_means[1,] - listener_age_means[2,]) / 2
# correlation between listener means and age effects
cor (listener_effects, listener_age_effects)
## [1] -0.8691We can develop some intuitions regarding correlations by considering the very simple vectors seen below. The elements of the second vector are exactly equal to twice every element of the first vector: They are perfectly predictable one from the other. As a result, these two vectors have a correlation of 1.
x1 = c(-1, -1, 1, 1)
y1 = c(-2, -2, 2, 2)
cor (x1, y1)
## [1] 1Below we see the opposite situation. The second vector is still twice the first vector, but now every sign differs across the two vectors. These are still perfectly predictable, just backward. For example, if a gambler were wrong 100% of the time, anyone who did the opposite would win every bet. Below, we see that these vectors have a correlation of −1.
x1 = c(-1, -1, 1, 1)
y1 = c( 2, 2, -2, -2)
cor (x1, y1)
## [1] -1In the next example, we see that the signs of each element of the second vector are totally unpredictable based on the corresponding element in the first vector. In half the cases the signs match and in half the cases they do not. This results in a correlation of 0 between the vectors.
x1 = c(-1, -1, 1, 1)
y1 = c(-2, 2, -2, 2)
cor (x1, y1)
## [1] 0Finally, we see a situation where the vectors almost match. In the example below, three of the four elements match in sign, resulting in a positive correlation between 0 and 1.
x1 = c(-1, -1, 1, 1)
y1 = c(-2, -2, -2, 2)
cor (x1, y1)
## [1] 0.57746.3.3 Random effects and the multivariate normal distribution
The multivariate normal distribution is a straightforward and very useful generalization of the normal distribution. A multivariate normal variable is a set of variables that are each normally distributed, and that result in another normally distributed variable when linearly combined. Each individual variable that makes up the multivariate normal represents a dimension of the multivariate normal. So, if we have a three-dimensional normal distribution with dimensions \(x_1, x_2\), and \(x_3\), this implies that: (1) Each of \(x_1, x_2\), and \(x_3\) is normally distributed, and (2) If we define a new variable \(x_4\) such that \(x_4 = a \cdot x_1 + b \cdot x_2 + c \cdot x_3\), where \(a, b,\) and \(c\) can take any scalar value, then \(x_4\) will be normally distributed.
When our models feature multiple predictors for a factor whose levels are estimated with adaptive pooling (e.g. speaker, listener), we model the coefficients with a multivariate normal distribution. In doing so we estimate the standard deviation of each dimension and the correlation between all pairs of dimensions. The easiest way to see why the correlation between dimensions matters is by drawing bivariate (two-dimensional) normal variables with different correlations and plotting the results.
The dimensions of the multivariate normal can have arbitrarily different means and standard deviations, but their marginal distributions will always be a (univariate) normal. In Figure 6.4 we plot randomly-generated samples from three different bivariate normal distributions differing in the correlation between their dimensions, one variable presented in each row. The variables all have means and standard deviations that reflect the distribution of listener means (first column), and the listener-dependent age effects (second column). So, the first dimension has a mean and standard deviation equal to 154 and 4.8 cm, and the second dimension has a mean and standard deviation equal to 10.1 and 4.2 cm, respectively.
show plot code
#mean (listener_means)
#sd (listener_means)
#mean (listener_age_effects)
#sd (listener_age_effects)
set.seed(.1)
par (mfrow = c(3,3), mar = c(4,4,1,1))
ranefs = phonTools::rmvtnorm (10000, means = c(153,10), sigma = matrix (c(4.8^2,0,0,4.3^2),2,2))
hist (ranefs[,1],main='',col=4,xlab='Intercept',freq = FALSE,breaks=40, xlim = c(130,175))
hist (ranefs[,2],main='',col=4,xlab='A1',freq = FALSE,breaks=40, xlim = c(-5,25))
plot (ranefs, pch=16,col=4,xlim=c(130,180),ylim=c(-10,27),xlab='Intercept',
ylab='A1')
phonTools::sdellipse (ranefs,add = TRUE, lwd=2,col=2,stdev =3)
grid()
ranefs = phonTools::rmvtnorm (10000, means = c(153,10), sigma = matrix (c(4.8^2,10.5,10.5,4.3^2),2,2))
hist (ranefs[,1],main='',col=4,xlab='Intercept',freq = FALSE,breaks=40, xlim = c(130,175))
hist (ranefs[,2],main='',col=4,xlab='A1',freq = FALSE,breaks=40, xlim = c(-5,25))
plot (ranefs, pch=16,col=4,xlim=c(130,180),ylim=c(-10,27),xlab='Intercept',
ylab='A1')
phonTools::sdellipse (ranefs,add = TRUE, lwd=2,col=2,stdev =3, xlim = c(145,175))
grid()
ranefs = phonTools::rmvtnorm (10000, means = c(153,10), sigma = matrix (c(4.8^2,-17.8,-17.8,4.3^2),2,2))
hist (ranefs[,1],main='',col=4,xlab='Intercept',freq = FALSE,breaks=40, xlim = c(130,175))
hist (ranefs[,2],main='',col=4,xlab='A1',freq = FALSE,breaks=40, xlim = c(-5,25))
plot (ranefs, pch=16,col=4,xlim=c(130,180),ylim=c(-10,27),xlab='Intercept',
ylab='A1')
phonTools::sdellipse (ranefs,add = TRUE, lwd=2,col=2,stdev =3, xlim = c(145,175))
grid()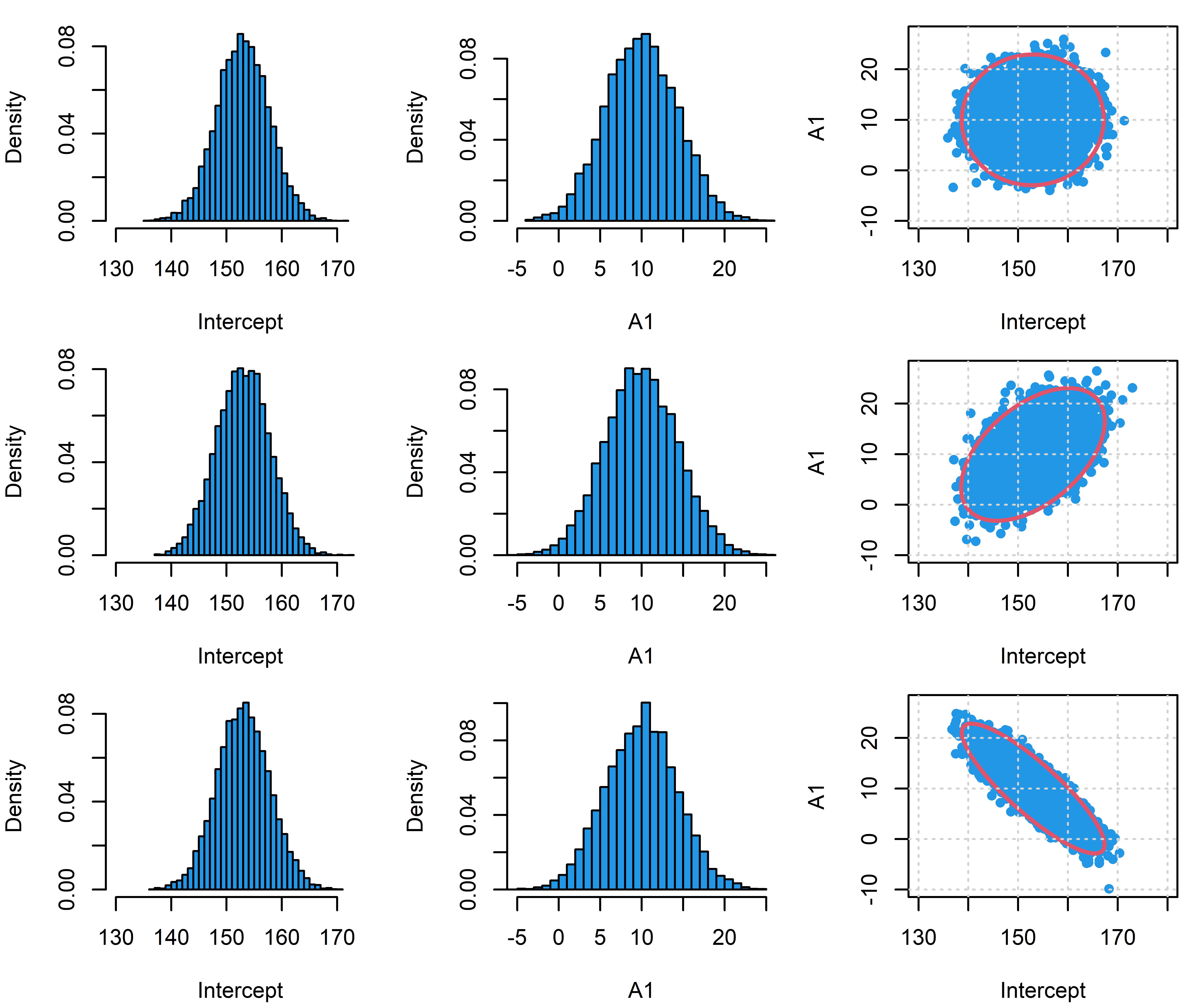
We can use the simulated variables presented in Figure 6.4 to imagine possible relationships between listener means and age effects across a large sample of listeners. In the absence of any correlation between variables (top row), the distribution will resemble a circle in two dimensions (if the standard deviations are equal). When there is a positive correlation between the two dimensions (middle row), the joint-distribution looks like an ellipse tilted up (moving from left to right). When there is a negative correlation (bottom row), the ellipse is tilted down moving left to right. Note, however, that the marginal distributions of the variables (illustrated in the left and middle columns) don’t change as the correlation changes. The correlation is a reflection of the joint variation in the two variables and will not be evident in the marginal distributions of each variable.
Understanding the correlations between your ‘random effect’ parameters is important because it helps you understand which combinations of parameter values are more or less likely. When our dimensions are uncorrelated it is difficult (if not impossible) to make useful predictions from one dimension to the other. For example, in the top row, we see that a mean height of 140 cm is about equally likely to be paired with apparent age affects (A1) of 0 or 20 cm. As a result, knowing that the speaker mean is 140 cm does not provide you much information about whether the age effect for that listener is likely to be large or small, positive or negative.
However, when the dimensions are correlated we can use this to make better predictions using our data. For example, in the bottom row, we see a strong negative correlation between our dimensions. As a result, an average height of 140 cm is very likely when age effects are 20 cm, but extremely unlikely to be seen with an age effect of 0 cm. So, in this case, knowing the speaker mean would actually help you narrow down the range of plausible listener effects. For this reason, when more than one random effect is estimated for each grouping factor, these are usually treated as a multivariate normal variable rather than as a set of independent normal distributions (as in our model in Equation 6.1).
6.3.4 Specifying priors for a multivariate normal distribution
The shape of the multivariate normal distribution (i.e. how much it looks like a circle vs a tilted ellipse in the bivariate case) is determined by a covariance matrix, often represented by a capital sigma (\(\mathrm{\Sigma}\)). A covariance matrix will be a square \(n \cdot n\) matrix for a variable with \(n\) dimensions. In Equation 6.6, we see an example of a covariance matrix for variables x, y, and z. The elements on the main diagonal of the covariance matrix represent the variances of each dimension, while the off-diagonal elements represent the co-variances of the variables (where \(\sigma_{x,y}=\sigma_{y,x}\)).
\[ \begin{equation} \begin{split} \Sigma = \begin{bmatrix} \sigma_{x}^2 & \sigma_{x,y} & \sigma_{x,z} \\ \sigma_{y,x} & \sigma_{y}^2 & \sigma_{y,z} \\ \sigma_{z,x} & \sigma_{z,y} & \sigma_{z}^2 \end{bmatrix} \\ \end{split} \end{equation} \tag{6.6}\]
Consider two random effects, a random by subject intercept \(L\), and a random by-listener apparent age effect called \(A \colon L\). If we assumed these came from a bivariate normal distribution the covariance matrix associated with this distribution might be:
\[ \begin{equation} \begin{split} \Sigma = \begin{bmatrix} \sigma_{L}^2 & \sigma_{L,A \colon L} \\ \sigma_{A \colon L, L} & \sigma_{A \colon L}^2 \\ \end{bmatrix} \\ \end{split} \end{equation} \tag{6.7}\]
When we dealt with unidimensional normal distributions for our previous random effects, we specified priors for the (unidimensional) standard deviations using t (or normal) distributions. The specification of priors for our covariance matrix is only slightly more complicated. Rather than specify priors for \(\mathrm{\Sigma}\) directly, brms (and Stan) builds up \(\mathrm{\Sigma}\) from some simpler components that we specify. The covariance matrix for our random effects is created by multiplying the standard deviations of our individual dimensions by a correlation matrix (\(R\)) specifying the correlations between each dimension. The operation is presented in Equation 6.8.
\[ \begin{equation} \begin{split} \mathrm{\Sigma} = \begin{bmatrix} \sigma_{L}^2 & \sigma_{L,A \colon L} \\ \sigma_{A \colon L, L} & \sigma_{A \colon L}^2 \\ \end{bmatrix} = \begin{bmatrix} \sigma_{L} & 0 \\ 0 & \sigma_{A \colon L} \\ \end{bmatrix} \cdot R \cdot \begin{bmatrix} \sigma_{L} & 0 \\ 0 & \sigma_{A \colon L} \\ \end{bmatrix} \\ \end{split} \end{equation} \tag{6.8}\]
The non-zero values in the outside matrices are the (marginal, univariate) standard deviations of the random intercepts (\(\sigma_{L}\)) and age effects (\(\sigma_{A \colon L}\)). The correlation matrix \(R\) contains information about the correlation between the dimensions of the variable (e.g. \(r_{L , A \colon L}\)). The correlation matrix \(R\) will look like Equation 6.9 for a two-dimensional variable. In a correlation matrix each row gives you information about the correlation of one dimension with the others. For example, the first row represents the correlation of the first dimension to itself (first column) and the second dimension (second column). Correlation matrices contain only values of 1 on the main diagonal since the correlation of something with itself is one. Since the correlation of \(x\) and \(y\) equals the correlation of \(y\) and \(x\), correlation matrices are symmetric. This means that in the two dimensional case \(r_{1,2}=r_{2,1}\), or, more generally, \(r_{i, j} = r_{j, i}\).
\[ \begin{equation} \begin{split} R = \begin{bmatrix} 1 & r_{L,A \colon L} \\ r_{A \colon L,L} & 1 \\ \end{bmatrix} \\ \\ \end{split} \end{equation} \tag{6.9}\]
When we have multiple random effects that we are modeling as a multivariate normal, we need to specify priors for the standard deviations of each individual dimension and for the correlations between each pair of dimensions (i.e. for the correlation matrix), but not for the covariance matrix \(\mathrm{\Sigma}\) directly. We provide priors for the standard deviations of the individual dimensions in the same way as we do for ‘unidimensional’ random effects. We specify priors for correlation matrices using the \(\mathrm{LKJCorr}\) distribution in brms.
\[ \begin{equation} \begin{split} R \sim \mathrm{LKJCorr} (\eta) \end{split} \end{equation} \tag{6.10}\]
This distribution has a single parameter (eta, \(\eta\)) that determines how peaked the distribution is around 0 (seen in Figure 6.5). Basically, higher numbers make it harder to find larger correlations (and therefore yield more conservative estimates).
show plot code
colours = colorRampPalette(bmmb::cols[colls = c(9,7,4,3,8,5,12)])(10)
tmp = lkjcorrdensity (1)
par (mar = c(4,4,1,.5), mfrow = c(1,2))
plot (tmp, type = 'l', col = colours[1], ylab="Density",xlab="Correlation",
ylim = c(0,2.5), xaxs='i', lwd=3, yaxs='i')
for (j in 1:10){
tmp = lkjcorrdensity (j)
lines (tmp, col = colours[j], lwd=3)
}
legend (0.65,2.5, legend = c(1:10),col = colours,
pch=15, bty = 'n', cex = 0.75)
plot (tmp[,1],log(tmp[,2]), type = 'l', col = colours[1], ylab="Log Density",xlab="Correlation",
ylim = c(-10,2), xaxs='i', lwd=3, yaxs='i')
for (j in 1:10){
tmp = lkjcorrdensity (j)
lines (tmp[,1],log(tmp[,2]), col = colours[j], lwd=3)
}
The above was a full explanation of what information the model needs and why it needs it. You don’t need to understand any of the above to use random effects correctly. The important take away is that whenever you are estimating any random effects above and beyond a random intercept, you need to:
Specify priors for the standard deviation of each dimension.
Specify a prior for the correlation matrix for the multivariate normal used for the random parameters.
And brm (and Stan) will do the rest.
6.3.5 Updating our model description
Now that we’ve discussed using multivariate normal distributions for our random effects, we can update our model formula as in Equation 6.11. Only two things have changed with respect to the description in Equation 6.1. First, the listener random effects are drawn from a multivariate normal distribution (\(\mathrm{MVNormal}\)) rather than as independent univariate normal variables. Second, we specify a prior for our correlation matrix (\(\mathrm{LKJCorr}\)). Notice that we do not directly specify a prior for the multivariate normal covariance matrix \(\mathrm{\Sigma}\). This is because, as noted above, Stan constructs \(\mathrm{\Sigma}\) by multiplying the standard deviation for each dimension (\(\sigma_{A \colon L}\) and \(\sigma_{L}\)) by the correlation matrix (\(R\)) as in Equation 6.8. We include this in the final line of the model for completeness, but will be excluding it from future model specifications. This is because this element is not specified by the user, and becomes increasingly bulky as our models become more complicated.
\[ \begin{equation} \begin{split} height_{[i]} \sim \mathrm{t}(\nu,\mu_{[i]},\sigma) \\ \mu_{[i]} = \mathrm{Intercept} + A + L_{[\mathsf{L}_{[i]}]} + A \colon L_{[\mathsf{L}_{[i]}]} + S_{[\mathsf{S}_{[i]}]} \\ \\ \mathrm{Priors:} \\ S_{[\bullet]} \sim \mathrm{N}(0,\sigma_S) \\ \begin{bmatrix} L_{[\bullet]} \\ A \colon L_{[\bullet]} \end{bmatrix} \sim \mathrm{MVNormal} \left( \begin{bmatrix} 0 \\ 0 \\ \end{bmatrix}, \mathrm{\Sigma} \right) \\ \\ \mathrm{Intercept} \sim \mathrm{t}(3,156,12) \\ A \sim \mathrm{t}(3,0,12) \\ \sigma, \sigma_L, \sigma_{A \colon L}, \sigma_S \sim \mathrm{t}(3,0,12) \\ \nu \sim \mathrm{gamma}(2, 0.1) \\ R \sim \mathrm{LKJCorr} (2) \\\\ \mathrm{\Sigma} = \begin{bmatrix} \sigma_{L} & 0 \\ 0 & \sigma_{A \colon L} \\ \end{bmatrix} \cdot R \cdot \begin{bmatrix} \sigma_{L} & 0 \\ 0 & \sigma_{A \colon L} \\ \end{bmatrix} \\ \end{split} \end{equation} \tag{6.11}\]
Here’s a plain English description of the model specification in Equation 6.11:
We are modeling apparent height as coming from a t-distribution with unknown nu (\(\nu\)), mean (\(\mu\)), and scale (\(\sigma\)) parameters. The expected value for any given trial (\(\mu\)) is modeled as the sum of an intercept, an effect for apparent age (\(A\)), a listener effect (\(L\)), a listener dependent effect for apparent age (\(A \colon L\)), and a speaker effect (\(S\)). The speaker effects were drawn from a univariate normal distribution with a standard deviation (\(\sigma_S\)) estimated from the data. The two listener effects were drawn from a bivariate normal distribution with standard deviations (\(\sigma_L, \sigma_{A \colon L}\)) and a correlation matrix (\(R\)) that was estimated from the data. The remainder of the ‘fixed’ effects and the bivariate correlation were given prior distributions appropriate for their expected range of values.
6.3.6 Fitting and interpreting the model
Below we fit a model where age coefficients vary across listeners. Notice that the only change in the formula is the inclusion of the A predictor on the left-hand-side of the pipe in (A|L). We now include a prior for a new class of parameter cor which applies to the correlation matrices for our multivariate normal variables. In addition, we specify the priors outside the brm function call, and pass this to the function.
# Fit the model yourself
priors = c(brms::set_prior("student_t(3,156, 12)", class = "Intercept"),
brms::set_prior("student_t(3,0, 12)", class = "b"),
brms::set_prior("student_t(3,0, 12)", class = "sd"),
brms::set_prior("lkj_corr_cholesky (2)", class = "cor"),
brms::set_prior("gamma(2, 0.1)", class = "nu"),
brms::set_prior("student_t(3,0, 12)", class = "sigma"))
model_re_t =
brms::brm (height ~ A + (A|L) + (1|S), data = notmen, chains = 4,
cores = 4, warmup = 1000, iter = 5000, thin = 4,
prior = priors, family = "student")# Or download it from the GitHub page:
model_re_t = bmmb::get_model ('6_model_re_t.RDS')We can check out the summary of our model:
bmmb::short_summary (model_re_t)And see that although many parameter values may have changed with respect to model_sum_coding_t from Chapter 5, the only new information is in the L group-level effects:
## Group-Level Effects:
## ~L (Number of levels: 15)
## Estimate Est.Error l-95% CI u-95% CI
## sd(Intercept) 4.34 0.84 3.05 6.29
## sd(A1) 4.26 0.85 2.96 6.25
## cor(Intercept,A1) -0.80 0.12 -0.95 -0.51This section of the model summary now includes an estimate of the standard deviation of the by-listener effect for age (sd(A1), i.e. the standard deviation of the listener by age interaction, \(\sigma_{A \colon L}\) in Equation 6.11), and the correlation between our listener-dependent intercept and age-effect terms (cor(Intercept,A1)). We can see that the estimate of this correlation (-0.80) is very similar to the ‘simple’ estimate we found above (-0.85).
You can get information about the variance, correlation, and covariance parameters using the VarCorr function in the brms package. As with the fixef and ranef functions, this function returns summaries of these samples by default but you can set summary=FALSE to get the individual samples for these parameters. We’re not going to talk about the structure of this output, but we encourage you to investigate it using the str function.
varcorr_information = brms::VarCorr (model_re_t)
str (varcorr_information)You can also use the get_corrs and get_sds functions in the bmmb package to get summaries of your model standard deviations (including the error term):
bmmb::get_sds (model_re_t)
## Estimate Est.Error Q2.5 Q97.5 group
## Int.L 4.338 0.8356 3.050 6.289 L
## A1 4.258 0.8463 2.964 6.248 L
## Int.S 3.057 0.3594 2.398 3.808 S
## sigma 5.354 0.2057 4.958 5.770 sigmaAnd correlations:
# specify that we want the correlations for L
bmmb::getcorrs (model_re_t, factor="L")
## Estimate Est.Error Q2.5 Q97.5
## A1, Int. -0.8018 0.1151 -0.9491 -0.5087Below we load the sum-coded, t-distributed model we fit in Chapter 5. This model contained an identical fixed-effects structure to model_re_t, but does not include listener-dependent age effects (and associated parameters).
model_sum_coding_t = bmmb::get_model ('5_model_sum_coding_t.RDS')Figure 6.6 presents a comparison of the two models, for selected model parameters. Despite clear similarities between the models, there are some changes to the credible intervals around the parameters that are shared across both models (presented in Figure 6.6). It can be risky to make up explanations for things after the fact (post hoc), but we can try to think about why these changes may have occurred. The change in the interval around the intercept is very small, and likely reflects our (slightly) better overall understanding of the data. In contrast, the interval around A1 has grown substantially. This is likely because we are now acknowledging between-listener variation in the A1 parameter, which model_sum_coding_t ignored (or treated as zero). model_re_t predicts a standard deviation of 4.3 cm in the A1 effect between listeners, and our data includes judgments from only 15 unique listeners. This limits how precise our A1 estimate can/should be.
show plot code
varcorr_information = brms::VarCorr (model_re_t)
comparison = rbind (brms::fixef(model_sum_coding_t),
brms::VarCorr (model_sum_coding_t)$L$sd,
brms::VarCorr (model_sum_coding_t)$residual__$sd,
brms::fixef(model_re_t),
varcorr_information$L$sd[1,],
varcorr_information$residual__$sd)
par (mfrow = c(1,4), mar = c(2,2,3,1), oma = c(0,3,0,0))
bmmb::brmplot (comparison[c(1,5),], ylim = c(152,159),main="Intercept",
xlim = c(.75,2.25), col = c(4,2), labels = "",cex.axis=1.2)
bmmb::brmplot(comparison[c(2,6),], ylim = c(6,11),main="A1",
xlim = c(.75,2.25), col = c(4,2), labels = "",cex.axis=1.2)
bmmb::brmplot(comparison[c(3,7),], ylim = c(2,8),main="sigma_L",
xlim = c(.75,2.25), col = c(4,2), labels = "",cex.axis=1.2)
bmmb::brmplot(comparison[c(4,8),], ylim = c(4,9.5),main="sigma",
xlim = c(.75,2.25), col = c(4,2), labels = "",cex.axis=1.2)
legend (1.1, 9, legend = c("Age RE", "No age RE"), col = c(2,4),
pch=16,bty='n', cex = 1.1,pt.cex=1.5)
mtext (side = 2, outer = TRUE, "Centimeters",adj = .46, cex=0.9, line = 1.2)
The standard deviation of our listener intercepts (\(\sigma_L\), ‘sigma_L’ in the figure) appears to decrease slightly at the inclusion of random effects for age. This is likely because what previously seemed like variation in listener averages may have actually been variation in listener age effects. The separation of this into two separate predictors may lead to the magnitude of variation in one being diminished. Finally, the decrease in the data-level error (\(\sigma\), ‘sigma’ in the figure) is due to the inclusion of the listener random effects for A1, and the fact that including listener-dependent values for A1 helped explain our variable. The error is just what the model can’t explain, so as our models explain more, the error will tend to get smaller.
6.4 Model Comparison
Bayesian models allow you to fit rather complicated ‘bespoke’ models to your data. A potential problem with this is that at some point your model may be ‘good enough’ such that, although further tweaks could be made, they are no longer contributing any practical benefit to your model. In fact, you can build a model that is so good at predicting your data that it can actually become bad at understanding the subject of your investigation more generally.
An analogy can be made between model fitting and clothing made by a tailor for an individual. You can go to a tailor and get a shirt made that exactly fits your body proportions. Imagine that tailoring the perfect shirt for a human body usually involved adjusting ten ‘shirt parameters’ (e.g. torso circumference, torso to sleeve ratio, etc.) to ensure a perfect fit for an individual. Despite this, when you go to a store to buy a shirt, there is usually one ‘parameter’, size, and it often comes in a small number of variants (e.g. small, medium, large). Since the shirts vary only in a small number of ways, they are very unlikely to fit any individual perfectly.
Why do stores intentionally sell clothing that doesn’t fit people as well as they could? Because the store is interested in selling clothes that fit everyone pretty well, rather than selling clothes that fit everyone perfectly. If stores sold shirts that fit everyone perfectly, each shirt model would only be useful to a very small number of people and would be useless for a large number of people. In contrast, by having a small number of shirts that fit the most people ‘pretty well’, the store can carry a small number of models and apply them successfully to customers in general.
This problem is sometimes referred to as the bias-variance tradeoff. In this case bias refers to the model’s ability to represent the ‘true’ relationship underlying the data, and variance refers to the degree to which the model is stable across data sets. Models that fit data very well (i.e. they have a low bias) often change substantially when fit to new data sets (i.e. they have a high variance). This is analogous to the fact that the shape of two shirts perfectly tailored (low bias) for two different people will potentially be very different from each other (high variance). On the other hand, models that do not fit the data too well (higher bias) often also have more consistent properties across new data sets (lower variance). This is analogous to the fact that shirts that vary in terms of small, medium, and large don’t fit many people perfectly, but manage to fit everyone pretty well while varying only slightly.
The bias-variance tradeoff can be understood in terms of the prediction of in-sample and out-of-sample data. Your in-sample data is the data you used to fit your model, and the out-of-sample data is other data that you do not have access to. A statistical model is overfit when it corresponds too closely to your in-sample data to the detriment of its ability to explain out-of-sample data. Recall that our models are usually used to carry out inductive reasoning: Going from a limited number of observations to the general case. In light of this, overfitting a model is exactly contrary to the goals of inductive inference. A model that does a poor job of generalizing to new observations is not useful to carry out induction. Further, a model that cannot explain out-of-sample data will not hold up to replication, which should be a concern for any researcher. This is because a researcher carrying out a replication of your work will necessarily be working with data that, from your perspective, is out-of-sample data.
In this section we will offer a high-level conceptual understanding of Bayesian model comparison, along with an explanation of how to carry this out. For more information on the subject we recommend reading Chapter 7 of the excellent Statistical Rethinking (McElreath, 2020). Much of the information provided in this section is provided in more detail in Gelman et al. (2014), and Vehtari et al. (2017).
6.4.1 In-sample and out-of-sample prediction
In order to compare models in a quantitative way, we need some value that can be calculated for different models that captures how ‘good’ the model is. For Bayesian models, we begin with what is called the log pointwise predictive density, abbreviated \(\mathrm{lpd}\) (or \(\mathrm{lppd}\)). The \(\mathrm{lpd}\) can be calculated in several ways, but Equation 6.12 presents an example of the general case. The \(\mathrm{lpd}\) is the sum of the logarithm of the density for each of your data points. The symbol \(\theta\) represents posterior estimates of all of the estimated parameters necessary to determine the probability density over each data point. This can be thought of as the general case of the log-likelihood outlined for the normal distribution in Section 2.7.1.
\[ \begin{equation} \widehat{\mathrm{lpd}} = \sum_{i=1}^{N} \mathrm{log} (p(y_{[i]} | \theta)) (\#eq-6-8) \end{equation} \tag{6.12}\]
The definition of \(\widehat{\mathrm{lpd}}\) bears a strong resemblance to the log posterior density, discussed in Section 3.8. Since we are adding logarithmic values, we know we are multiplying the underlying probabilities. If the data points are independent given our parameter values, then \(\mathrm{lpd}\) represents the joint density of observing the data given the model structure and the parameter estimates (\(\theta\)). Although prior probabilities are not included in this calculation they do factor into the estimation of \(\theta\), and as a result do have an effect on values of \(\mathrm{lpd}\).
Because \(\mathrm{lpd}\) is a logarithmic value, large negative values are closer to zero on the original scale. So, values of \(\mathrm{lpd}\) closer to (or above) zero represent models that are more likely given the data. As a result, we might think that we should simply select the model with the highest \(\mathrm{lpd}\) as our ‘best’ model. However, \(\mathrm{lpd}\) does not tell us directly about expected out-of-sample prediction, which is what we often care about.
We can think about out-of-sample prediction in terms of the expected log pointwise predictive density, abbreviated \(\mathrm{elpd}\) (or \(\mathrm{elppd}\)), presented in Equation 6.13. Unlike the \(\mathrm{lpd}\), the \(\mathrm{elpd}\) is defined in terms of hypothetical out-of-sample data (\(\tilde{y}\)) instead of the in-sample data (\(y\)). The \(\mathbb{E}\) below represents the expected value function (discussed in Section 2.5.1). So, the \(\mathrm{elpd}\) represents the expected value of \(\mathrm{lpd}\) for out-of-sample data.
\[ \begin{equation} \mathrm{elpd} = \sum_{i=1}^{N} \mathbb{E}(\mathrm{log} (p(\tilde{y}_i | \theta))) \end{equation} \tag{6.13}\]
Of course, you can’t actually know the value of \(\mathbb{E}(\mathrm{log} (p(\tilde{y}_i | \theta))\) because you do not have access to the true properties of the out-of-sample data (\(\tilde{y}\)). As a result, you must settle for an estimate of \(\mathrm{elpd}\), \(\widehat{\mathrm{elpd}}\). The simplest, and worst, way to estimate out-of-sample prediction is by simply looking at the in-sample prediction. One of the reasons that this does not really work is because making models more and more complicated will always improve in-sample prediction, at least a little. However, if the predictors are not related to true characteristics of the processes underlying the data, they will also tend to decrease the fit of the model to new data. Returning to the analogy of shirt fits discussed above. You can buy a shirt from the store and take it to a tailor to get it customized. The more the tailor changes this from the ‘standard’ shape, the better the shirt will fit you and the worse it will fit everyone else. Only alterations which conform to the ‘true’ average torso shape will increase the fit for people in general (and may in fact reduce the fit for you).
We can demonstrate this for some very simple models using simulations. In the code below, we generate three random variables consisting only of the values -1 and 1. We then use only the first variable (x1), and random normally-distributed error, to simulate two sets of random data: Our in-sample (y) data, and our out-of-sample data (y_tilde). We then fit three models to only the in-sample data. These models include increasingly more predictor variables (\(x_1, x_2, x_3\)), however, we know that only \(x_1\) is useful to understand the underlying process. Finally, we tried to predict the in-sample data and the out-of-sample data using the parameters estimated for each model using only the in-sample data.
n = 50 # how many observations
iter = 1000 # how many simulations
# these will hold the model log likelihoods for each iteration
lpd_hat = matrix (0, iter, 3)
elpd_hat = matrix (0, iter, 3)
set.seed(1)
for (i in 1:iter){
# create 3 random predictors
x1 = sample (c(-1,1), n, replace=TRUE)
x2 = sample (c(-1,1), n, replace=TRUE)
x3 = sample (c(-1,1), n, replace=TRUE)
# generate the observed (in sample) data with an
# underlying process that only uses the x1 predictor
y = 1 + x1 + rnorm (n, 0, 1)
# use the same process to simulate some "out-of-sample" data
y_tilde = 1 + x1 + rnorm (n, 0, 1)
for (j in 1:3){
# fit three models, the first using the real underlying model
if (j==1) mod = lm (y ~ 1+x1)
# the next two include random useless predictors
if (j==2) mod = lm (y ~ 1+x1 + x2)
if (j==3) mod = lm (y ~ 1+x1 + x2 + x3)
# find the predicted value (mu) for each data point
mu = mod$fitted.values
# and the estimated sigma parameter
sigma = summary(mod)$sigma
# equivalent to equation 6.10
lpd_hat[i,j] = sum (dnorm (y, mu, sigma, log = TRUE))
# equivalent to equation 6.11
elpd_hat[i,j] = sum (dnorm (y_tilde, mu, sigma, log = TRUE))
}
}The models above are fit using a function that we have not discussed to this point. The lm (linear model) function uses maximum-likelihood estimation (see Section 2.8) to fit regression models with relatively simple (‘unilevel’, see Figure 4.2) structures. We use it here because it estimates regression parameters very quickly and therefore is reasonable to use when we want to fit 3000 models in 5 seconds or so.
For each of our three candidate models, we use the predicted values (mu, \(\mu\)) and error estimates (sigma, \(\sigma\)) obtained using our in-sample data to estimate \(\widehat{\mathrm{lpd}}\) using the in sample data:
\[ \begin{equation} \widehat{\mathrm{lpd}} = \sum_{i=1}^{N} \mathrm{log} (\mathrm{N}(y_{[i]} | \mu, \sigma)) \end{equation} \tag{6.14}\] And \(\widehat{\mathrm{elpd}}\) using our out-of-sample data:
\[ \begin{equation} \widehat{\mathrm{elpd}} = \sum_{i=1}^{N} \mathrm{log} (\mathrm{N}(\tilde{y}_i | \mu, \sigma)) \end{equation} \tag{6.15}\]
In the formulas above we replace \(p(y_i | \theta)\) with \(\mathrm{N}(y_{[i]} | \mu, \sigma)\) because the simulations generate normally-distributed data. Our simulations result in three sets of \(\widehat{\mathrm{lpd}}\) and three sets of \(\widehat{\mathrm{elpd}}\), a pair of each for each of the models above. The average of each of these six sets of values is presented in the left plot of Figure 6.7. Since logarithmic values closer to zero are closer to one on the original scale, more negative log-likelihood values indicate a less likely outcome. We can see that the \(\widehat{\mathrm{lpd}}\) improves as the model becomes more complicated, despite the fact that the \(x_1\) and \(x_2\) had absolutely no relationship to the data generating process or to the dependent variable.
show plot code
means = round (apply (cbind(lpd_hat,elpd_hat), 2, mean),1)
layout (mat=t(c(1:3)), widths = c(.4,.4,.2))
par (mar = c(4.2,1,1,.1),oma = c(.5,3.5,.1,.1))
plot (means[1:3], type = "b", lwd = 2, ylim = range(means)+c(-.5,.5),xaxt='n',
pch=16, xlim = c(.8,3.2), ylab = "lpd",xlab="Predictors",
cex.lab=1.3,cex.axis=1.3)
axis (side=1,at=1:3,labels = c("x1","x1, x2","x1, x2, x3"),cex.axis=1.3)
lines (means[4:6], col =2, lwd=2, type = "b",pch=16)
arrows (1,means[1]-0.2, 1,means[4]+0.2,code=3, length=0.1,lwd=2)
arrows (2,means[2]-0.2, 2,means[5]+0.2,code=3, length=0.1,lwd=2)
arrows (3,means[3]-0.2, 3,means[6]+0.2,code=3, length=0.1,lwd=2)
text ((1:3)+.1, -71, labels = round(c(means[1]-means[4],means[2]-means[5],
means[3]-means[6]),2),cex=1.2)
text (0.8,c(-68.8,-73.6), labels = c("More Likely","Less likely"), pos=4,cex=1.2)
mtext (side=2,text = "Log density", line = 3)
#legend (3.4,-70.5, legend= c("In sample","out-of-sample"),
# col=c(1,2), lwd=2,bty="n")
plot (means[1:3], type = "b", lwd = 2, ylim = range(means)+c(-.5,.5),xaxt='n',
pch=16, xlim = c(.8,3.2), ylab = "",xlab="Predictors",yaxt="n",cex.lab=1.3)
axis (side=1,at=1:3,labels = c("x1","x1, x2","x1, x2, x3"),cex.axis=1.3)
lines (means[4:6], col =2, lwd=2, type = "b",pch=16)
lines (means[1:3] - c(2:4), col =2, lwd=2, type = "b",pch=16, lty = 2)
arrows (1,means[1]-0.2, 1,means[1]+0.2-2,code=3, length=0.1,lwd=2)
arrows (2,means[2]-0.2, 2,means[2]+0.2-3,code=3, length=0.1,lwd=2)
arrows (3,means[3]-0.2, 3,means[3]+0.2-4,code=3, length=0.1,lwd=2)
text (1:3, means[1:3]+.25, labels = means[1:3],cex=1.2)
text (1:3, means[4:6]-.25, labels = means[4:6],cex=1.2)
text (1:3, means[1:3]-.25-c(2:4), labels = means[1:3]-c(2:4),cex=1.2)
plot (0, bty='n', xaxt='n',yaxt='n',xlab="",type="n")
legend (.6,.2,legend = c("lpd_hat","elpd_hat","elpd_adj"), lwd=4,
col = c(1,2,2),cex=1.4,lty = c(1,1,3), bty='n')
elpd_adj) based on the number of predictors in the model, as discussed in the text.
Why does this happen? One way to think about it is that the tallest person in California and Arizona will be at least as tall as the tallest person in Arizona. By increasing the number of ways it can explain your data, your more complex model will do at least as well as the model with fewer possible explanations. However, although the extra parameters increase the \(\widehat{\mathrm{lpd}}\) estimate, they actually decrease values of \(\widehat{\mathrm{elpd}}\), indicating a worse out of sample fit. Why? Because since the extra predictors included in our model in no way relate to our data, the ‘answers’ they provide can only be due to overfitting, the learning of characteristics that are specific to the in-sample data rather than consistent properties of the out-of-sample data.
So, we see that adding ‘unnecessary’ predictors can decrease our out-of-sample performance. Ok, maybe we should just not ever include any ‘unnecessary’ predictors in our models? This is a bit like suggesting that since putting is hard, one should try to get a hole-in-one whenever possible. Obviously this would be ideal, however, there are some complications. In the example in Figure 6.7 we knew the true underlying model and generated out-of-sample data that exactly conformed to the characteristics of our in-sample data. In real life, researchers do not usually have access to out-of-sample data, they do not know the characteristics of the ‘true’ model that underlies their data, nor can they confirm that any out-of-sample data shares the exact underlying process as their in-sample data. As a result, we can never really know what the difference is between in sample and out-of-sample prediction for our models.
Despite these complications, you may have noticed that: 1) The slopes of the lines representing \(\widehat{\mathrm{elpd}}\) and \(\widehat{\mathrm{lpd}}\) in Figure 6.7 seem to have predictable slopes, and 2) The lines diverge from each other at predictable rates based on the complexity of the models. Statisticians have noticed this too, and have used this to adjust \(\widehat{\mathrm{lpd}}\) in order to estimate values of \(\widehat{\mathrm{elpd}}\) for out-of-sample data.
6.4.2 Out-of-sample prediction: Adjusting predictive accuracy
The logic of adjusting \(\widehat{\mathrm{lpd}}\) based on model complexity can be understood with reference to Figure 6.7. Our goal is to select the model with the best out-of-sample prediction (i.e. the highest value on the red line), given only knowledge of the in-sample prediction (the values on the black line). In the left plot we can see that the difference between the black and red lines for each model increases by approximately one for every parameter we add. Let’s assume for the time being that this is a general property of all models. Since our models had two, three, and four parameters (including the intercept) respectively let’s subtract two, three and four from their respective \(\widehat{\mathrm{lpd}}\) estimates to arrive at adjusted \(\widehat{\mathrm{elpd}}\) estimates for each model. We can think of this as penalizing the value of \(\widehat{\mathrm{lpd}}\) based on some penalty value \(\mathrm{p}\) as in Equation 6.16. Different ways to estimate \(\widehat{\mathrm{elpd}}\) differ in terms of how they estimate \(\widehat{\mathrm{lpd}}\) and \(\mathrm{p}\).
\[ \begin{equation} \widehat{\mathrm{elpd}} = \widehat{\mathrm{lpd}} - \mathrm{p} \end{equation} \tag{6.16}\]
You may have noticed that our penalization does not exactly recreate the line reflecting \(\mathrm{elpd}\) in Figure 6.7, but rather results in a line parallel to it. We can never know the real distance between \(\mathrm{lpd}\) and \(\mathrm{elpd}\), the solid red and black lines in Figure 6.7, because we can never know the ‘true’ properties of out-of-sample data. Despite this, penalization allows us to estimate a line parallel to \(\mathrm{elpd}\) (the broken red line in Figure 6.7), and base our inference on this line. In the simple example we are discussing here, we are setting \(\mathrm{p}=k\), where \(k\) is the number of parameters estimated by the model. If we carry out the operation in Equation 6.16 using the values in Figure 6.7, we arrive at values of \(\mathrm{elpd}\) of -71.7 (-69.7 - 2) and -72.7 (-68.7-4) for the least and most complex models. Based on these estimates of \(\widehat{\mathrm{elpd}}\), we expect that the model with the worst \(\widehat{\mathrm{lpd}}\) actually has the best \(\mathrm{elpd}\).
In fact, we know that in this case the ‘best’ model corresponds exactly to the true data generating process. However, penalization will not always result in the highest values of \(\widehat{\mathrm{elpd}}\) for the simplest model. In Figure 6.8 we simulate new fake data, except now we include \(x_2\) in the ‘real’ underlying data generating process (i.e. y = x1 + x2 + rnorm (n, 0, 1)). As a result, for this data we actually do need both \(x_1\) and \(x_2\) in the model. As seen below, penalization does not obscure the benefit of adding \(x_2\) to our model when it is warranted. This is because the relatively small penalty associated with the increased model complexity does not overwhelm the large benefit due to the inclusion of a predictor that is actually related to our dependent variable.
show plot code
n = 50 # how many observations
iter = 1000 # how many simulations
# these will hold the model log likelihoods for each iteration
in_sample_ll = matrix (0, iter, 3)
out_of_sample_ll = matrix (0, iter, 3)
set.seed(1)
for (i in 1:iter){
# create 3 random predictors
x1 = sample (c(-1,1), n, replace=TRUE)
x2 = sample (c(-1,1), n, replace=TRUE)
# generate the observed (in sample) data with an
# underlying process that only uses the x1 predictor
y_in = 1 + x1 + rnorm (n, 0, 1)
# use the same process to simulate some "out-of-sample" data
y_out = 1 + x1 + rnorm (n, 0, 1)
for (j in 1:3){
# fit three models, the first using the real underlying model
if (j==1) mod = lm (y_in ~ 0+x1)
# the next two include random useless predictors
if (j==2) mod = lm (y_in ~ 1+x1)
if (j==3) mod = lm (y_in ~ 1+x1 + x2)
# find the predicted value (mu) for each data point
yhat = mod$fitted.values
# and the estimated sigma parameter
sigma = summary(mod)$sigma
in_sample_ll[i,j] = sum (dnorm (y_in, yhat, sigma, log = TRUE))
out_of_sample_ll[i,j] = sum (dnorm (y_out, yhat, sigma, log = TRUE))
}
}
means = round (apply (cbind(in_sample_ll,out_of_sample_ll), 2, mean),1)
layout (mat=t(c(1:3)), widths = c(.4,.4,.2))
par (mar = c(4,1.5,1,.1),oma = c(.5,3,.1,.1))
plot (means[1:3], type = "b", lwd = 2, ylim = range(means)+c(-.5,.5),xaxt='n',
pch=16, xlim = c(.8,3.2), ylab = "",
xlab="Predictors",cex.lab=1.3,cex.axis=1.3)
axis (side=1,at=1:3,labels = c("x1","x1, x2","x1, x2, x3"),cex.axis=1.3)
lines (means[4:6], col =2, lwd=2, type = "b",pch=16)
mtext (side=2,text = "Log density", line = 3)
#legend (3.4,-70.5, legend= c("In sample","out-of-sample"),
# col=c(1,2), lwd=2,bty="n")
plot (means[1:3], type = "b", lwd = 2, ylim =c(-73.5,-69),xaxt='n',
pch=16, xlim = c(.8,3.2), ylab = "",xlab="Predictors",
yaxt="n",cex.lab=1.3)
axis (side=1,at=1:3,labels = c("x1","x1, x2","x1, x2, x3"),cex.axis=1.3)
lines (means[4:6], col =2, lwd=2, type = "b",pch=16)
lines (means[1:3] - c(1:3), col =2, lwd=2, type = "b",pch=16, lty = 2)
arrows (1,means[1]-0.2, 1,means[1]+0.2-1,code=3, length=0.1,lwd=2)
arrows (2,means[2]-0.2, 2,means[2]+0.2-2,code=3, length=0.1,lwd=2)
arrows (3,means[3]-0.2, 3,means[3]+0.2-3,code=3, length=0.1,lwd=2)
text (c(1,2.2,3), means[1:3]+.25, labels = means[1:3],cex=1.2)
text (c(1,2.2,3), means[4:6]-.25, labels = means[4:6],cex=1.2)
text (c(1,2.2,3), means[1:3]-.25-c(1:3), labels = means[1:3]-c(1:3),cex=1.2)
plot (0, bty='n', xaxt='n',yaxt='n',xlab="",type="n")
legend (.6,.2,legend = c("lpd_hat","elpd_hat","elpd_adj"), lwd=4,
col = c(1,2,2),cex=1.4,lty = c(1,1,3))
x2) in the data generating process. (right) The same values as on the left, however, now elpd is estimated based on adjusting the lpd using the number of model parameters. The y axis range intentionally omits the first model so that the information for the second and third models can be seen clearly.
Two aspects involved in the traditional estimation of \(\widehat{\mathrm{elpd}}\) need to be updated to use these measures for multilevel Bayesian models. The first of these is the way that models are penalized based on their complexity. Historically, the \(\mathrm{p}\) term is related to the number of independent parameters estimated by the model. Estimated parameters are those that are not specified a priori but instead depend on the data and structure of the model. Unfortunately, counting the number of independent parameters is not so straightforward in our multilevel models since parameters estimated with adaptive pooling (and shrinkage) are not fully independent. For example, a set of 10 ‘random effects’ that have all been pulled slightly toward their shared mean can hardly be considered totally independent. On the other hand they do vary from each other in unpredictable ways. As a result, it seems like a random effect with ten levels may represent somewhere between zero and ten independent parameters, based on how much they have been shrunk toward their mean. Our estimate of \(\widehat{\mathrm{elpd}}\) will need a way to estimate model complexity that takes this into account.
Second, \(\widehat{\mathrm{lpd}}\) and \(\mathrm{p}\) have traditionally been point estimates, single values often based on maximum-likelihood estimation. Since our models consist of posterior distributions of parameters, we instead have distributions of \(\widehat{\mathrm{lpd}}\) and \(\mathrm{p}\). This means that we also have a distribution of values of \(\widehat{\mathrm{elpd}}\), and it would be useful to take this into account.
In this section we’re only going to discuss the widely available information criterion (\(\mathrm{WAIC}\)) as calculated using the brms package. For a more complete treatment of other methods (and historical approaches), please see Gelman et al. (2014). To calculate \(\mathrm{WAIC}\) we first find the average density of each data point (\(i\)) given our model parameters (\(p(y|\theta^s)\)) across all posterior samples (\(S\)). This is presented for data point 1 in Equation 6.17. For example, imagine a case where we have 5000 posterior draws so that \(S=5000\). To calculate the value below for our first data point (\(y_{[1]}\)) we would find the density for every one of the 5000 posterior draws based on the changing values of \(\theta^s\) across our draws. The average of these values is represented in Equation 6.17.
\[ \begin{equation} \frac{1}{S} \sum_{s=1}^{S} p(y_{[1]} | \theta^s) \end{equation} \tag{6.17}\]
To estimate \(\widehat{\mathrm{lpd}}\) for a set of \(n\) data points we take the logarithm of the value in Equation 6.17 and add this up across all of our observations. This is presented in Equation 6.18.
\[ \begin{equation} \widehat{\mathrm{lpd}} = \sum_{i=1}^{n} \mathrm{log} (\frac{1}{S} \sum_{s=1}^{S} p(y_{[i]} | \theta^s)) \end{equation} \tag{6.18}\]
Rather than count the number of parameters in our model, \(\mathrm{WAIC}\) estimates the penalty term based on the characteristics of the predictive density. First, you find the log density for each individual data point across all posterior draws, and then find the variance of this. Equation 6.19 shows an example of this for the first data point. The \(Var_{s=1}^{\,S}\) term indicates that we are finding the variance of \(\mathrm{log} (p(y_{[1]} | \theta^s))\) across values of \(S\).
\[ \begin{equation} \mathrm{Var}_{s=1}^{\,S}(\mathrm{log} (p(y_{[1]} | \theta^s))) \end{equation} \tag{6.19}\]
To estimate the penalty terms for WAIC, \(\mathrm{p_{WAIC}}\), the value in Equation 6.19 is added up for all \(n\) data points as in Equation 6.20.
\[ \begin{equation} \mathrm{p_{\mathrm{WAIC}}} = \sum_{i=1}^{n} \mathrm{Var}_{s=1}^{\,S}(\mathrm{log} (p(y_{[i]} | \theta^s))) \end{equation} \tag{6.20}\]
Why does this work? This is one of those things that you may need to get used to rather than understand, although more information can be found in Vehtari et al. (2017). The short, conceptual explanation is that more complex models exhibit more variation in their posterior probabilities. As a result, the variance of the log density across the posterior samples is a general way to estimate model complexity that avoids issues related to how many truly independent parameters a model estimates. Given our estimate of \(\widehat{\mathrm{lpd}}\) and \(\mathrm{p_{WAIC}}\), we can now estimate \(\widehat{\mathrm{elpd}}_{WAIC}\) as in Equation 6.21.
\[ \begin{equation} \widehat{\mathrm{elpd}}_{WAIC} = \widehat{\mathrm{lpd}} - \mathrm{p_{WAIC}} \end{equation} \tag{6.21}\]
Below we load the sum-coded models we fit in Chapter 5:
model_sum_coding = bmmb::get_model ('5_model_sum_coding.RDS')
model_sum_coding_t = bmmb::get_model ('5_model_sum_coding_t.RDS')And set our options to sum coding to match the coding we used when we fit the models:
options (contrasts = c('contr.sum','contr.sum'))We can use the add_criterion function in brms, and specify criterion="waic" to add the waic criterion to our model object. We do this for both of our models.
model_sum_coding =
brms::add_criterion (model_sum_coding, criterion="waic")
model_sum_coding_t =
brms::add_criterion (model_sum_coding_t, criterion="waic")Adding the waic criterion to our model with Gaussian errors (model_sum_coding) returns an error message. To understand why we get these errors we can investigate the model waic information, which we can see below:
model_sum_coding$criteria$waic
##
## Computed from 5000 by 1401 log-likelihood matrix
##
## Estimate SE
## elpd_waic -5042.3 32.5
## p_waic 81.8 3.7
## waic 10084.6 65.0
##
## 27 (1.9%) p_waic estimates greater than 0.4. We recommend trying loo instead.The first two rows represent the expected log pointwise predictive density (\(\widehat{\mathrm{elpd}}_{WAIC}\), elpd_waic), and the penalty related to the flexibility of the model (\(\mathrm{p_{WAIC}}\), p_waic). The third column is the information criterion \(\mathrm{WAIC}\) which is just -2 times the first row. The \(\mathrm{p_{WAIC}}\) penalty term is sometimes referred to as the effective number of parameters, but Vehtari et al. (2017) caution that this usage is somewhat figurative and should not be ‘over-interpreted’. The effective number of parameters relates to the complexity and flexibility of the model and its ability to adapt to new data. Our sum coding model has 114 estimated parameters: 15 listener means, 1 listener standard deviation, 94 speaker means, 1 speaker standard deviation, 2 fixed effects terms, and one error standard deviation. Despite this, we see that our effective number of parameters is just 81.8.
The statistics provided above are calculated individually for each data point. We can get the pointwise information as seen below:
model_waic_info = model_sum_coding$criteria$waic$pointwise
model_t_waic_info = model_sum_coding_t$criteria$waic$pointwiseThere will be one row for each data point used to fit the model. Below we can have a look at the first six values:
# first six data points
head (model_waic_info)
## elpd_waic p_waic waic
## [1,] -5.108 0.234948 10.216
## [2,] -3.116 0.004170 6.232
## [3,] -4.431 0.153398 8.862
## [4,] -3.109 0.003014 6.217
## [5,] -4.139 0.116198 8.279
## [6,] -3.104 0.002666 6.208The estimates above simply correspond to the sum of each column. The standard error (SE) corresponds to the variance of the column times the square root of the number of rows (since the statistics are sums and not means). Based on this, we can recreate the summary values seen above:
# the sum of each column
colSums (model_waic_info)
## elpd_waic p_waic waic
## -5042.3 81.8 10084.6
# the standard deviation of each column
apply (model_waic_info,2,sd) * sqrt(1401)
## elpd_waic p_waic waic
## 32.511 3.742 65.021Now we can return to the issue of the error message, which said that “27 (1.9%) p_waic estimates greater than 0.4”. Large values of p_waic suggest a poor fit between a data point and the model. To investigate this we can get the posterior mean residuals from each of the models we are considering:
resids = scale(residuals(model_sum_coding)[,1])
resids_t = scale(residuals(model_sum_coding_t)[,1])We scale our residuals so that they are represented in terms of standard deviations from the mean, and plot these against the p_waic values calculated for each data point by each model. Clearly, large residuals relate to large p_waic values. In other words, large p_waic values are related to data points that are a very poor fit for our model. In our model with Gaussian errors this relationship is very predictable and quickly leads to large values in p_waic. However, for our model with t-distributed errors (model_sum_coding_t), residuals beyond two standard deviations do not strongly affect p_waic. These differences are due to the different behaviors of the normal and t-distributions in their tails, as discussed in Section 5.9.
show plot code
par (mfrow = c(1,2), mar = c(4,4,1,1))
plot(model_sum_coding$criteria$waic$pointwise[,2], resids,xlab="p_waic",ylab="Residual",
ylim = c(-4.5,4.5), xlim = c(0,1.1), col=cols[6],pch=16)
grid()
abline (v = 0.4)
#abline (h=c(-2.5,2.5))
plot(model_sum_coding_t$criteria$waic$pointwise[,2], resids_t,xlab="p_waic",ylab="Residual",
ylim = c(-4.5,4.5), xlim = c(0,1.1), col=cols[6],pch=16)
grid()
abline (v = 0.4)
model_sum_coding. (right) The same as on the left but for the model with t-distributed errors, model_sum_coding_t.
The warning message suggest that we use loo (discussed in the next section) rather than waic because some p_waic values are too large. Why is this bad? Because the theory underlying the use of \(\widehat{\mathrm{elpd}}_{WAIC}\) basically assumes that there will not be large values of p_waic. So, if there are large values of p_waic that suggests that something is wrong and \(\widehat{\mathrm{elpd}}_{WAIC}\) may no longer be reliable. When this occurs, as the error message suggests, you shouldn’t use \(\widehat{\mathrm{elpd}}_{WAIC}\) even if it seems reliable and looks ‘fine’. Think of it this way, if a bridge says it has a weight limit of three tonnes and you’re driving a truck that weighs four tonnes, should you drive across the bridge? Maybe you get across safely and save some time. Maybe you crash off the bridge into the river. When you use something like this despite being warned not to, you run the same risk: Maybe what you report is a true and reliable analysis, and maybe it’s not and you are reporting nonsense (the academic equivalent of crashing into the river).
6.4.3 Out-of-sample prediction: Cross validation
The last way to evaluate models that we’ll be discussing is called cross validation. Cross validation consists of dividing your data into two groups. You use one group to fit a model (i.e. your in-sample, or training data), and then use this model to predict the other group of data (i.e. the out-of-sample, or testing data). In this way, cross validation is a way to simulate out-of sample prediction using only the data you actually have.
There are many ways to carry out cross validation, and these mostly differ in the way that data is divided into training and testing groups. Holdout cross validation makes one single partition and uses one group to test and the other to train. Obviously this is not ideal because the results will be highly dependent on the specific groups you made. In k-fold cross validation you split your data into \(k\) equal parts. You then train on parts \(k_{-i}\) for iteration \(i\), and predict the \(i^{th}\) group using that model. This approach can minimize the problems of holdout cross validation since it uses k, rather than one, estimates of the out-of-sample performance.
The logical endpoint of k-fold cross-validation is leave-one-out cross validation, sometimes referred to as \(\mathrm{LOO}\). In leave-one-out cross validation you leave out a single observation at a time. So, if you have \(n\) observations you train the model on all observations but \(i\) (i.e. \(y_{[-i]}\)), and then predict the lone held out point (\(y_[i]\)). Although \(\mathrm{LOO}\) provides excellent estimates of out-of-sample prediction, this approach can be computationally intensive since it involves fitting \(n\) models for \(n\) data points. For example, our relatively small data set (notmen) has 1401 observations, potentially requiring 1401 models.
Luckily, recent advances have resulted in fast ways to approximate \(\widehat{\mathrm{elpd}}_{LOO}\), i.e. estimates of \(\widehat{\mathrm{elpd}}\) based on \(\mathrm{LOO}\), without having to refit models repeatedly. The loo package (Vehtari et al. 2022) in R and the associated functions implemented in brms make it easy to estimate \(\widehat{\mathrm{elpd}}_{LOO}\) in a very fast an efficient manner. In addition, \(\mathrm{LOO}\) works in many cases where \(\mathrm{WAIC}\) does not, hence the suggestion in the error message above to use \(\mathrm{LOO}\) for model comparison.
The calculation of \(\widehat{\mathrm{elpd}}_{LOO}\) is more complicated than what we can explain here, however, we can provide an approximate definition. In Equation 6.22 we use the \(\approx\) symbol because we are not providing an exact definition of how \(\widehat{\mathrm{elpd}}_{LOO}\) is calculated in practice, but only in principle. Equation 6.22 states that the estimate of \(\mathrm{elpd}\) provided by LOO cross validation is approximately equal to the sum of the log density of each data point (\(y_{[i]}\)) based on parameters estimated using all the data except for that point (\(\theta_{y_{[-i]}}\)).
\[ \begin{equation} \widehat{\mathrm{elpd}}_{LOO} \approx \sum_{i=1}^{n} \mathrm{log} (p(y_{[i]} | \theta_{y_{[-i]}})) \end{equation} \tag{6.22}\]
We define the relationship between \(\widehat{\mathrm{elpd}}_{LOO}\) and \(\widehat{\mathrm{lpd}}\) using the same general relationship outlined above, updated for \(\mathrm{LOO}\) in Equation 6.23.
\[ \begin{equation} \widehat{\mathrm{elpd}}_{LOO} = \widehat{\mathrm{lpd}} - \mathrm{p_{\mathrm{LOO}}} \end{equation} \tag{6.23}\]
Based on this, we can estimate \(\mathrm{p_{\mathrm{LOO}}}\) by rearranging the terms of the equation as seen in Equation 6.24. Just as with \(\mathrm{p_{\mathrm{WAIC}}}\), \(\mathrm{p_{\mathrm{LOO}}}\) reflects the effective number of parameters, an estimate of model complexity.
\[ \begin{equation} \mathrm{p_{\mathrm{LOO}}} = \widehat{\mathrm{lpd}} - \widehat{\mathrm{elpd}}_{LOO} \end{equation} \tag{6.24}\]
Estimates of \(\widehat{\mathrm{elpd}}_{LOO}\) and associated statistics can be added to our models using the code below. We will now include our model with random effects for apparent age in our comparison.
model_sum_coding =
brms::add_criterion (model_sum_coding, criterion="loo")
model_sum_coding_t =
brms::add_criterion (model_sum_coding_t, criterion="loo")
model_re_t =
brms::add_criterion (model_re_t, criterion="loo")We can see our new criteria using the code below. Notice that we no longer see the error message we got with \(\mathrm{WAIC}\).
model_sum_coding$criteria$loo
##
## Computed from 5000 by 1401 log-likelihood matrix
##
## Estimate SE
## elpd_loo -5042.7 32.5
## p_loo 82.2 3.8
## looic 10085.4 65.1
## ------
## Monte Carlo SE of elpd_loo is 0.2.
##
## All Pareto k estimates are good (k < 0.5).
## See help('pareto-k-diagnostic') for details.Since we no longer have warnings, we can compare our models as seen below. This comparison contrasts the values of \(\widehat{\mathrm{elpd}}_{LOO}\) for each data point across all our models. It presents the sum of the difference, and the standard error of that sum, relative to the best performing model. Below, model_re_t has an elpd_diff of 0, indicating that this is the best model according to this measure.
brms::loo_compare (model_sum_coding,
model_sum_coding_t,
model_re_t, criterion = "loo")
## elpd_diff se_diff
## model_re_t 0.0 0.0
## model_sum_coding_t -204.4 19.2
## model_sum_coding -224.1 19.6What does the value of zero mean? It only means that this is our ‘reference point’. The value of \(\widehat{\mathrm{elpd}}_{LOO}\) for our best model is:
model_re_t$criteria$loo$estimates[1,]
## Estimate SE
## -4818.63 37.15So, if we set this value to zero then we can express the corresponding estimates for the other models relative to this value. Values of elpd_diff for model_sum_coding_t and model_sum_coding are -204 and -222 respectively, indicating substantial differences in \(\widehat{\mathrm{elpd}}_{LOO}\) between our models. Specifically, they are around 200 less than our best model (so around -5000, as seen above). We can explore where these values come from by extracting the pointwise information from our models just as we did for \(\mathrm{WAIC}\).
model_loo_info = model_sum_coding$criteria$loo$pointwise
model_t_loo_info = model_sum_coding_t$criteria$loo$pointwise
model_re_t_lo_info = model_re_t$criteria$loo$pointwiseWe can see that the elpd_diff is just the sum of the difference in elpd estimates across the two models:
sum(model_t_loo_info[,1]-model_re_t_lo_info[,1])
## [1] -204.4The standard error of the difference is simply the standard deviation of the difference times the square root of the number of observations.
sd(model_t_loo_info[,1]-model_re_t_lo_info[,1]) * sqrt(1401)
## [1] 19.21We can use this knowledge to calculate the difference between our two worst performing models since these are not directly compared above:
sum(model_loo_info[,1]-model_t_loo_info[,1])
## [1] -19.64
sd(model_loo_info[,1]-model_t_loo_info[,1]) * sqrt(1401)
## [1] 7.578And see that these values correspond to those obtained using the ‘official’ comparison function as seen below:
brms::loo_compare (model_sum_coding, model_sum_coding_t, criterion = "loo")
## elpd_diff se_diff
## model_sum_coding_t 0.0 0.0
## model_sum_coding -19.6 7.6Finally, we can check out the estimated number of parameters by summing the third column of our pointwise information, which contains information about \(\mathrm{p_{\mathrm{LOO}}}\) for each model. We can compare this to the actual number of parameters estimated by our models. An easy way to find the number of estimated parameters is to get the posterior draws for a model using the get_samples function from bmmb. This will return a data frame that contains one column for each estimated parameter, plus two columns for the lp and lprior (discussed in Section 3.8). So, if we find the number of columns minus two, we can quickly count the number of estimated parameters for most kinds of models. However, keep in mind that this works as of the writing of this sentence (October 14th, 2022), and the output of software can change. It’s worth checking your expectations before taking shortcuts like this, for example by confirming the number of columns and seeing the information contained in each column before using this method to report the number of parameters.
Below, we compare the actual number of parameters for each model with our effective number of parameters. For example, we can see that going from Gaussian to t-distributed errors results in the estimation of one additional ‘real’ parameter (\(\nu\)), but the number of ‘effective’ parameters goes up by about 3. Adding random effects for apparent age to our model required the addition of 17 parameters: 15 listener-specific age effects, a standard deviation for these effects, and the correlation between the listener specific age and intercept effects. However, we can see that this has led to an increase of about 24 effective parameters. We can potentially explain this by thinking about how the inclusion of random effects for apparent age may have affected the estimation of the other random effects already included in the model. However, we are not going to worry too much and ‘over-interpret’ the effective number of parameters.
# Actual and effective number of parameters for simplest model
ncol(bmmb::get_samples(model_sum_coding))-2
## [1] 114
sum(model_loo_info[,'p_loo'])
## [1] 82.17
# Actual and effective number of parameters for t model
ncol(bmmb::get_samples(model_sum_coding_t))-2
## [1] 115
sum(model_t_loo_info[,'p_loo'])
## [1] 85.23
# Actual and effective number of parameters for 'random effects' model
ncol(bmmb::get_samples(model_re_t))-2
## [1] 132
sum(model_re_t_lo_info[,'p_loo'])
## [1] 109.16.4.4 Selecting a model
Which model should we use? Based on the comparison above, we see that model_re_t has an \(\widehat{\mathrm{elpd}}\) that is 204 greater than the next best model. How large does an \(\widehat{\mathrm{elpd}}\) difference need to be in order to be meaningful? There are two things that need to be taken into account: The magnitude of a difference and the uncertainty in the difference. A general rule of thumb seems to be that a difference of around 4 in \(\widehat{\mathrm{elpd}}\) suggests a meaningful difference between the models (Vehtari et al. 2017). However, this is simply a general guideline and doesn’t mean that a difference of 3.99 does not matter and a difference of 4.01 does. On the other hand, even large differences between models may not be reliable in the presence of large standard errors (i.e. large amounts of variation in the difference). For example, below we see the difference between our two smaller models:
brms::loo_compare (model_sum_coding, model_sum_coding_t, criterion = "loo")
## elpd_diff se_diff
## model_sum_coding_t 0.0 0.0
## model_sum_coding -19.6 7.6The difference is 19.6, which is obviously large enough to be considered a meaningful improvement in the model. However, the standard error is 7.6. This means that the difference is only about 2.6 standard errors from zero. How many standard errors away from zero does a difference need to be in order to be ‘real’? This is impossible to say, and in fact the ‘reality’ of any given model can not be definitively established by any statistical test. Ok, so how many standard errors from zero should it be before we make a fuss about it? The answer to this seems to be somewhere in the neighborhood of 2-4 at least. If we think of improvements to our model as continuous, we can think of differences that are two standard errors away as potentially ‘less reliable’ and differences that are >5 standard errors away as ‘more reliable’.
However, \(\mathrm{elpd}\) is just a tool and is not really meant to be used to select the ‘best’ or ‘real’ model from a set of alternatives. The decision about which model to use is up to the researcher and can’t be handed off to the models themselves. In addition to considering differences in \(\widehat{\mathrm{elpd}}\) in isolation, the researcher should also consider how theoretically or practically warranted differences in their models are. For example, we know that our data contains way too many outliers to have proper normally distributed errors. Based on previous experience, we knew a priori that outliers are typical for listener judgements of things like apparent height. As a result, although the improvement provided by using t-distributed errors is not large, we may choose to keep using t-distributed errors in our model anyways. On the other hand, given the small difference between the estimates provided by both models and the not-huge difference in \(\widehat{\mathrm{elpd}}\) between the models, a researcher may be warranted in simply using normally distributed errors in their model.
In contrast to these small differences, we see a difference of 204 in \(\widehat{\mathrm{elpd}}\) due to the addition of random effects for apparent age, 10.7 standard errors away from zero. Keep in mind this does not mean that a researcher must include this predictor nor that this structure will necessarily be an aspect of the real model. What it does mean is that: 1) The addition of random effects for apparent age greatly improves the fit of our model to our data, 2) This increase in fit is likely to extend to the data we did not observe, and 3) We have pretty good evidence that the difference between the models is reliable. We could add to this: 4) It makes sense that there would be listener-dependent variation in the effect for apparent age, for many reasons. As a result, in this situation it seems that random age effects should be included in our model.
Before finishing our discussion of model comparison, we want to show an example of a situation where adding a predictor does not help. To do this we add a useless predictor to our data frame, as below. This predictor is a random sample of -1 and 1 with no relationship to our height judgments. We can see below that the average reported height is basically the same for both values of our useless predictor.
set.seed(1)
notmen$useless = sample (c(-1,1),nrow(notmen), replace = TRUE)
tapply (notmen$height, notmen$useless, mean)
## -1 1
## 153 154Below we fit our t-distributed random effects model again, however, this time we include the useless predictor in the model formula, and even include a random effect for it:
height ~ A + useless + (A + useless|L) + (1|S)
We haven’t discussed including multiple predictors in our formulas yet, and in fact we will do so in Chapter 7. For now, we are only interested in considering how this useless predictor affects our model comparisons. We fit this model below:
# Fit the model yourself
options (contrasts = c('contr.sum','contr.sum'))
priors = c(brms::set_prior("student_t(3,156, 12)", class = "Intercept"),
brms::set_prior("student_t(3,0, 12)", class = "b"),
brms::set_prior("student_t(3,0, 12)", class = "sd"),
brms::set_prior("lkj_corr_cholesky (2)", class = "cor"),
brms::set_prior("gamma(2, 0.1)", class = "nu"),
brms::set_prior("student_t(3,0, 12)", class = "sigma"))
model_re_t_tooBig =
brms::brm (height ~ A + useless + (A + useless|L) + (1|S), data = notmen,
chains = 4, cores = 4, warmup = 1000, iter = 5000, thin = 4,
prior = priors, family = "student")And add the loo criterion to it.
model_re_t_tooBig = brms::add_criterion (model_re_t_tooBig, criterion="loo")Finally, we compare this to our equivalent model, minus the useless predictor.
brms::loo_compare (model_re_t, model_re_t_tooBig)
## elpd_diff se_diff
## model_re_t_tooBig 0.0 0.0
## model_re_t -0.7 2.8The more-complex model has a slightly higher \(\widehat{\mathrm{elpd}}\), but this difference is only 1/4 the magnitude of the standard error. In addition, we can look at a summary of the fixed effects and see that the value of the useless predictor is near zero (0.3), and the 95% credible interval is wide relative to this value and includes zero and very small values ([-.2, .8]).
brms::fixef(model_re_t_tooBig)
## Estimate Est.Error Q2.5 Q97.5
## Intercept 155.4454 1.1583 153.1882 157.7513
## A1 8.5267 1.1226 6.2757 10.7094
## useless 0.3362 0.2522 -0.1688 0.8357So, does this mean that this predictor should be excluded from the model? We would be justified in doing so, but may not necessarily want to. For example, if one of our important research questions centered on the value of the useless predictor, the fact that it is around zero and not some other value (e.g. -100) may be useful information. For example, we might want to keep the predictor in the model so we can say something like “So & So (2007) reported a value of -100 for the useless predictor. However, our results suggest that the effect of this predictor is likely to be near zero [mean = 0.34, sd = 0.25, 95% CI = [-0.17, 0.84])”.
6.5 Answering our research questions
We’ve selected the model with random effects as the ‘best’ model and are ready to revisit our research questions from Chapter 5 again:
(Q1) How tall do speakers perceived as adult females sound?
(Q2) How tall do speakers perceived as children sound?
(Q3) What is the difference in apparent height associated with the perception of adultness?
Our answers to the main research questions are largely unchanged from Section 5.12, however, there have been some changes that highlight interesting aspects of our data. We’re going to focus on what our model tells us about the listener dependent intercepts and effects for apparent age.
We saw that there was a strong negative correlation between the listener means and age effects. The reason for this is clearly evident in Figure 6.1. Listeners generally provided quite stable estimates for adult speakers. However, they exhibited substantial variation in their average judged height for child speakers. This makes sense. Most people probably have a good sense of approximately how tall adult females are on average. However, how tall are children 10-12? This is harder to answer for the average person. Not only is there more variability in height for children in these age ranges, but in addition most people are not around large numbers of children 10-12 and so may not have a good sense of how tall they are on average. Since reported adult heights are more or less fixed across listeners, listeners that indicated shorter children necessarily indicated shorter speakers overall. In addition, listeners that indicated shorter children also would tend to exhibit larger age effects. In this way, the listener means and age effect become negatively correlated.
Although we said we would stick to sum coding for this book, it is worth noting that this is actually a situation where it might make sense to use treatment coding, using adult as the reference level (see Section 5.6.1). This would not affect our answers to the questions above but it would make the structure of the model more closely reflect the structure of the data, and it would decrease the correlation between the listener-dependent random effects. Why? Because when the listener intercepts correspond to their adult means (and not the grand mean), the intercept no longer helps you predict their age effect. As we can see in Figure 6.1, all listeners rate adult speakers about the same height regardless of how tall/short they think the children are.
6.6 ‘Traditionalists’ corner
In traditionalists corner, we’re going to compare the output of brms to some more ‘traditional’ approaches. We’re not going to talk about the traditional models in any detail, the focus of this section is simply to highlight the similarities between different approaches, and to point out where to find equivalent information in the different models. If you are already familiar with these approaches, these sections may be helpful. If not, some of the information provided here may not make much sense, although it may still be helpful. If you want to know more about the statistical methods being discussed here, please see the preface for a list of suggested background reading in statistics.
6.6.1 Bayesian multilevel models vs. lmer
Here we compare the output of brms to the output of the lmer (linear mixed-effects regression) function, a very popular function for fitting multilevel models in the lme4 package in R. Below we fit a model that is analogous to our model_re_t model, save for the use of Gaussian rather than t-distributed errors. Since we set contrasts to sum coding using the options above, this will still be in effect for this model. If you have not done so, run the line:
options (contrasts = c("contr.sum","contr.sum"))Before fitting the model below so that its output looks as expected. We can fit a model with random age effects using lmer with the code below, and check out the model print statement.
# get data
notmen = bmmb::exp_data[exp_data$C_v!='m' & exp_data$C!='m',]
lmer_model = lme4::lmer (height ~ A + (A|L) + (1|S), data = notmen)
lmer_model
## Linear mixed model fit by REML ['lmerMod']
## Formula: height ~ A + (A | L) + (1 | S)
## Data: notmen
## REML criterion at convergence: 9890
## Random effects:
## Groups Name Std.Dev. Corr
## S (Intercept) 3.53
## L (Intercept) 4.12
## A1 3.98 -0.92
## Residual 7.67
## Number of obs: 1401, groups: S, 94; L, 15
## Fixed Effects:
## (Intercept) A1
## 155.05 8.64The model now includes estimates of the correlation between the listener random effects, and of the standard deviation of the listener-dependent age effects. Figure 6.10 is a comparison of the listener means and age effects fit by both approaches. Clearly the results are very similar save for the fact that just as with our correlations and standard deviations, brms gives us intervals while lmer only gives us point estimates.
show plot code
random_effects = brms::ranef(model_re_t)$L
par (mfrow = c(1,2), mar = c(4,4,1,1))
brmplot (random_effects[,,1], col = bmmb::cols,
ylab = "Listener effects (cm)", xlab="Listener")
points (lme4::ranef (lmer_model)$L[,1], pch=4,lwd=2, cex=3,
col = bmmb::cols)
abline (h=0,lty=3)
brmplot (random_effects[,,2], col = bmmb::cols, xlab="Listener",
ylab = "Listener age effects (cm)")
points (lme4::ranef (lmer_model)$L[,2], pch=4,lwd=2, cex=3,
col = bmmb::cols)
abline (h=0,lty=3)
6.7 Exercises
The analyses in the main body of the text all involve only the unmodified ‘actual’ resonance level (in exp_data). Responses for the stimuli with the simulate ‘big’ resonance are reserved for exercises throughout. You can get the ‘big’ resonance in the exp_ex data frame, or all data in the exp_data_all data frame.
Fit and interpret one or more of the suggested models:
Easy: Analyze the (pre-fit) model that’s exactly like
model_re_t, except using the data inexp_ex(bmmb::get_model("6_model_re_t_ex.RDS")).Medium: Fit a model like
model_re_t, but comparing any two groups across resonance levels.Hard: Fit two models like
model_re_t, but comparing any two groups across resonance levels. Compare results across models to think about group differences.
In any case, describe the model, present and explain the results, and include some figures. This time, also talk about the relationships between the random effects and any possible correlation between them.
6.8 References
Gelman, A., Hwang, J., & Vehtari, A. (2014). Understanding predictive information criteria for Bayesian models. Statistics and computing, 24(6), 997-1016.
McElreath, R. (2020). Statistical rethinking: A Bayesian course with examples in R and Stan. Chapman and Hall/CRC.
Vehtari, A., Gelman, A., & Gabry, J. (2017). Practical Bayesian model evaluation using leave-one-out cross-validation and WAIC. Statistics and computing, 27(5), 1413-1432.
Vehtari A, Gabry J, Magnusson M, Yao Y, Bürkner P, Paananen T, Gelman A (2022). “loo: Efficient leave-one-out cross-validation and WAIC for Bayesian models.” R package version 2.5.1, https://mc-stan.org/loo/.
